题目内容
数列{an}满足:a1=6,an+1=an2+4an+2,(n∈N*)
(Ⅰ)设Cn=log2(an+2),求证:{Cn}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设bn=
-
,数列{bn}的前n项和为Tn,求证:
≤Tn<
.
(Ⅰ)设Cn=log2(an+2),求证:{Cn}是等比数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设bn=
| 1 |
| an-2 |
| 1 | ||
|
| 7 |
| 30 |
| 1 |
| 4 |
考点:数列与不等式的综合,等比关系的确定
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ)把给出的数列递推式变形得到an+1+2=(an+2)2,两边取以2 为底数的对数证得答案;
(Ⅱ)求出(Ⅰ)中等比数列{Cn}的通项公式,代回Cn=log2(an+2)可得数列{an}的通项公式;
(Ⅲ)把bn=
-
化为bn=
-
,求和后代入首项和an+1即可证得答案.
(Ⅱ)求出(Ⅰ)中等比数列{Cn}的通项公式,代回Cn=log2(an+2)可得数列{an}的通项公式;
(Ⅲ)把bn=
| 1 |
| an-2 |
| 1 | ||
|
| 1 |
| an-2 |
| 1 |
| an+1-2 |
解答:
(Ⅰ)证明:由an+1=a
+4an+2,得an+1+2=(an+2)2,
∴log2(an+1+2)=2log2(an+2),
∵Cn=log2(an+2),
即Cn+1=2Cn,
∴数列{Cn}是以2为公比的等比数列;
(Ⅱ)解:∵a1=6,
∴C1=log2(a1+2)=log28=3,
则Cn=3•2n-1,即an+2=23•2n-1,
∴an=23•2n-1-2;
(Ⅲ)证明:把an=23•2n-1-2代入bn=
-
,
得:bn=
-
,
则Tn=(
-
)+(
-
)+…+(
-
)
=
-
=
-
.
∴
≤Tn<
.
2 n |
∴log2(an+1+2)=2log2(an+2),
∵Cn=log2(an+2),
即Cn+1=2Cn,
∴数列{Cn}是以2为公比的等比数列;
(Ⅱ)解:∵a1=6,
∴C1=log2(a1+2)=log28=3,
则Cn=3•2n-1,即an+2=23•2n-1,
∴an=23•2n-1-2;
(Ⅲ)证明:把an=23•2n-1-2代入bn=
| 1 |
| an-2 |
| 1 | ||
|
得:bn=
| 1 |
| an-2 |
| 1 |
| an+1-2 |
则Tn=(
| 1 |
| a1-2 |
| 1 |
| a2-2 |
| 1 |
| a2-2 |
| 1 |
| a3-2 |
| 1 |
| an-2 |
| 1 |
| an+1-2 |
=
| 1 |
| a1-2 |
| 1 |
| an+1-2 |
| 1 |
| 4 |
| 1 |
| 23•2n-4 |
∴
| 7 |
| 30 |
| 1 |
| 4 |
点评:本题是数列与不等式综合题,考查由递推式确定等比关系,训练了裂项相消法求数列的和,考查了由放缩法证明不等式,属中高档题.

练习册系列答案
相关题目
按照如图所示的算法框图,则输出的结果是( )


| A、1005 | B、1006 |
| C、1007 | D、1008 |
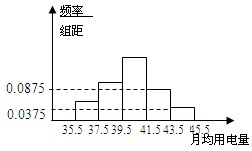 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3.
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如下;其中直方图从左到右前3个小矩形的面积之比为1:2:3. 如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心.
如图,矩形ABCD所在的平面和平面ABEF互相垂直,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,∠BAF=60°,O,P分别为AB,CB的中点,M为底面△OBF的重心. 如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,
如图在四棱锥P一ABCD中,底面ABCD为直角梯形,AD∥BC,∠BAD=90°,BC=2AD,AC与BD交于点O,点M,N分别在线PC、AB上,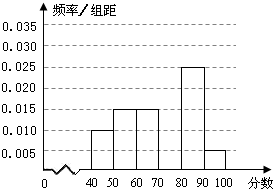 某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.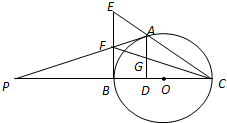 如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.
如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.