��Ŀ����
�躯��f��x��=lnx+ex��g��x��=ex+
x2-ax��a��R����e=2.71828������Ȼ�����ĵ�����
��1����F��x��=f��x��-g��x������F��x���ĵ������䣻
��2�����壺�������գ�x���ڶ�����Ϊ[m��n]��m��n���ϵ�ֵ��Ϊ[m��n]���������[m��n]Ϊ�����գ�x���ġ�ͬ�����䡱����a=
ʱ������F��x�������䣨0��2�����Ƿ���ڡ�ͬ�����䡱����˵�����ɣ�
��3����a��1ʱ���������䣨2��3����������������ȵ�ʵ��x1��x2����|f��x1��-f��x2��|��|g��x1��-g��x2��|��������a��ȡֵ��Χ��
| 1 |
| 2 |
��1����F��x��=f��x��-g��x������F��x���ĵ������䣻
��2�����壺�������գ�x���ڶ�����Ϊ[m��n]��m��n���ϵ�ֵ��Ϊ[m��n]���������[m��n]Ϊ�����գ�x���ġ�ͬ�����䡱����a=
| 3 |
| 2 |
��3����a��1ʱ���������䣨2��3����������������ȵ�ʵ��x1��x2����|f��x1��-f��x2��|��|g��x1��-g��x2��|��������a��ȡֵ��Χ��
���㣺���õ����о������ĵ�����
ר�⣺�¶���,�������ۺ�Ӧ��
��������1�����õ��������ĵ������伴�ɣ�
��2�����ݡ�ͬ�����䡱�Ķ���ó�
?����2lnx-x2+x=0�ڣ�0��2���ϴ������������ʵ�������õ���֤�����ɣ�
��3���ɣ�1����|f��x1��-f��x2��|=f��x2��-f��x1������|f��x1��-f��x2��|��|g��x1��-g��x2��|?f��x2��-f��x1����|g��x1��-g��x2��|?f��x1��-f��x2����g��x1��-g��x2����f��x2��-f��x1������f��x��-g��x�������䣨2��3������������f��x��+g��x�������䣨2��3��������������[f��x��-g��x��]���0��[f��x��+g��x��]���0�����õ����г�����ʽ��ü��ɣ�
��2�����ݡ�ͬ�����䡱�Ķ���ó�
|
��3���ɣ�1����|f��x1��-f��x2��|=f��x2��-f��x1������|f��x1��-f��x2��|��|g��x1��-g��x2��|?f��x2��-f��x1����|g��x1��-g��x2��|?f��x1��-f��x2����g��x1��-g��x2����f��x2��-f��x1������f��x��-g��x�������䣨2��3������������f��x��+g��x�������䣨2��3��������������[f��x��-g��x��]���0��[f��x��+g��x��]���0�����õ����г�����ʽ��ü��ɣ�
���
�⣺��1����F��x��=f��x��-g��x����F��x��=lnx-
x2+ax��
��F�䣨x��=
��������ɵ�F��x���Ķ�����Ϊ��0��+�ޣ���
��F�䣨x��=0⇒x1=
��x2=
���ɵ�x1��0��x2��0��
��F�䣨x����0⇒0��x��
��������F��x���ĵ�����������Ϊ��0��
����
��F�䣨x����0⇒x��
��������F��x���ĵ����ݼ�����Ϊ��
��+�ޣ���
��2����a=
ʱ��F��x��=lnx-
x2+
x�����䶨����Ϊ[m��n]��m��n����������ڡ�ͬ�����䡱���Ҷ�Ӧ��ֵ��Ϊ[m��n]��
�ɣ�1����֪F��x���ڣ�0��2���ϵ�������������
⇒
��
������lnx-
x2+
x=x�ڣ�0��2���ϴ������������ʵ����
������2lnx-x2+x=0�ڣ�0��2���ϴ������������ʵ����
��T��x��=2lnx-x2+x����T�䣨x��=
-2x+1����գ�x��=T�䣨x��=
-2x+1����ա䣨x��=-
-2�����ա䣨x����0�������
�ຯ���գ�x���ڣ�0��2���ϵ����ݼ����Ҧգ�e-1���T2e+1-
��0���գ�2��=-2��0��
�������䣨
��2���ϱش���Ψһ�ĵ�x0�ʣ�
��2����ʹ�æգ�x0��=0��
��x�ʣ�
��x0��ʱ���ա䣨x����0��T��x���ڣ�
��2���ϵ���������
��x�ʣ�x0��2��ʱ���ա䣨x����00��T��x���ڣ�x0��2���ϵ����ݼ���
��T��
��=
��0���գ�1��=1��0����x0��1����T��x���ڣ�1��x0������������
T��x0����T��1��=0��T��2��=2ln2-4+2=2ln2-2=2��ln2-1����0��
�ຯ��T��x��=2lnx-x2+x�����䣨
��2������������ȵĽ⣬
������2lnx-x2+x=0�ڣ�0��2���ϴ������������ʵ����
�ʺ���F��x���ڣ�0��2���ϴ��ڡ�ͬ�����䡱��
��3��������2��x1��x2��3���������f��x��=lnx+ex�����䣨2��3������������
����|f��x1��-f��x2��|=f��x2��-f��x1����
��|f��x1��-f��x2��|��|g��x1��-g��x2��|?f��x2��-f��x1����|g��x1��-g��x2��|
?f��x1��-f��x2����g��x1��-g��x2����f��x2��-f��x1����
��f��x1��-g��x1����f��x2��-g��x2����f��x1��+g��x1����f��x2��+g��x2���������
��f��x��-g��x�������䣨2��3������������f��x��+g��x�������䣨2��3������������
��[f��x��-g��x��]���0��[f��x��+g��x��]���0��
������ת��Ϊ������x�ʣ�2��3������
���������
⇒
��a��
+2e2��
| 1 |
| 2 |
��F�䣨x��=
| 1-x2+ax |
| x |
��F�䣨x��=0⇒x1=
a-
| ||
| 2 |
a+
| ||
| 2 |
��F�䣨x����0⇒0��x��
a+
| ||
| 2 |
a+
| ||
| 2 |
��F�䣨x����0⇒x��
a+
| ||
| 2 |
a+
| ||
| 2 |
��2����a=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
�ɣ�1����֪F��x���ڣ�0��2���ϵ�������������
|
|
������lnx-
| 1 |
| 2 |
| 3 |
| 2 |
������2lnx-x2+x=0�ڣ�0��2���ϴ������������ʵ����
��T��x��=2lnx-x2+x����T�䣨x��=
| 2 |
| x |
| 2 |
| x |
| 2 |
| x2 |
�ຯ���գ�x���ڣ�0��2���ϵ����ݼ����Ҧգ�e-1���T2e+1-
| 2 |
| e |
�������䣨
| 1 |
| e |
| 1 |
| e |
��x�ʣ�
| 1 |
| e |
| 1 |
| e |
��x�ʣ�x0��2��ʱ���ա䣨x����00��T��x���ڣ�x0��2���ϵ����ݼ���
��T��
| 1 |
| e |
| e(-2e+1)-1 |
| e2 |
T��x0����T��1��=0��T��2��=2ln2-4+2=2ln2-2=2��ln2-1����0��
�ຯ��T��x��=2lnx-x2+x�����䣨
| 1 |
| e |
������2lnx-x2+x=0�ڣ�0��2���ϴ������������ʵ����
�ʺ���F��x���ڣ�0��2���ϴ��ڡ�ͬ�����䡱��
��3��������2��x1��x2��3���������f��x��=lnx+ex�����䣨2��3������������
����|f��x1��-f��x2��|=f��x2��-f��x1����
��|f��x1��-f��x2��|��|g��x1��-g��x2��|?f��x2��-f��x1����|g��x1��-g��x2��|
?f��x1��-f��x2����g��x1��-g��x2����f��x2��-f��x1����
��f��x1��-g��x1����f��x2��-g��x2����f��x1��+g��x1����f��x2��+g��x2���������
��f��x��-g��x�������䣨2��3������������f��x��+g��x�������䣨2��3������������
��[f��x��-g��x��]���0��[f��x��+g��x��]���0��
������ת��Ϊ������x�ʣ�2��3������
|
|
| 8 |
| 3 |
| 5 |
| 2 |
������������Ҫ�������õ����жϺ����ĵ����������估�¸����⡢���������Ľ�����������黮��˼�롢��������˼��������������ۺ�������ǿ�������⣮

��ϰ��ϵ�д�
 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
�����Ŀ
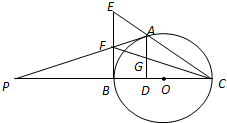 ��ͼ��A����BCΪֱ���ġ�O��һ�㣬AD��BC�ڵ�D������B����O�����ߣ���CA���ӳ����ཻ�ڵ�E��G��AD���е㣬����CG���ӳ���BE�ཻ�ڵ�F���ӳ�AF��CB���ӳ����ཻ�ڵ�P��
��ͼ��A����BCΪֱ���ġ�O��һ�㣬AD��BC�ڵ�D������B����O�����ߣ���CA���ӳ����ཻ�ڵ�E��G��AD���е㣬����CG���ӳ���BE�ཻ�ڵ�F���ӳ�AF��CB���ӳ����ཻ�ڵ�P�� ��ͼ��ʾ�������DZ߳�Ϊ1��С�����Σ��������ô�������ij�����������ͼ����ö������ȫ���Ϊ
��ͼ��ʾ�������DZ߳�Ϊ1��С�����Σ��������ô�������ij�����������ͼ����ö������ȫ���Ϊ