题目内容
已知数列{an}中,a1=1,前n项的和为Sn,对任意的n≥2(n∈N*),3Sn-4,an,2-
Sn-1总成等差数列.
(1)求a2,a3,a4的值并猜想数列{an}的通项公式an
(2)证明:
|ai|<2.
| 3 |
| 2 |
(1)求a2,a3,a4的值并猜想数列{an}的通项公式an
(2)证明:
| n |
 |
| i=1 |
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列
分析:(1)由已知可得,2an=3Sn-2-
Sn-1,当n≥2时,2an+1=3Sn+1-2-
Sn,两式相减可得an与an+1的递推公式,结合等比数列的通项公式可求通项公式an.
(2)表示才数列的前n项和,通过等比数列求和,推出结果即可.
| 3 |
| 2 |
| 3 |
| 2 |
(2)表示才数列的前n项和,通过等比数列求和,推出结果即可.
解答:
解:(1)a1=1,∵当n≥2时,3Sn-4,an,2-
Sn-1总成等差数列,
∴2an=3Sn-
sn-1-2.
再由a1=1,令n=2可得 2a2 =3s2-
a1-2,即 2an=3(1+a2 )-
-2,解得 a2=
.
令n=3 可得2a3=3S3-
S2-2,即 2a3=3(1+
+a3)-
(1+
)-2,解得 a3=-
.
同理,令n=4,可求得 a4=
?.
∴a2=
,a3=-
,a4=
∵当n≥2时,2an+2=3sn-
sn-1,∴2an+1+2=3sn+1-
sn.
两式相减,得2an+1 -2an=3an+1-
an,即
=-
,
∴a2,a3,…an,…成等比数列,故an=
.----(8分)
(2)∵
|ai|=|a1|+|a2|+|a3|+|a4|+…+|an|
=1+
+
+
+…+21-n
=
=2(1-
)<2------(12分)
| 3 |
| 2 |
∴2an=3Sn-
| 3 |
| 2 |
再由a1=1,令n=2可得 2a2 =3s2-
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
令n=3 可得2a3=3S3-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
同理,令n=4,可求得 a4=
| 1 |
| 8 |
∴a2=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
∵当n≥2时,2an+2=3sn-
| 3 |
| 2 |
| 3 |
| 2 |
两式相减,得2an+1 -2an=3an+1-
| 3 |
| 2 |
| an+1 |
| an |
| 1 |
| 2 |
∴a2,a3,…an,…成等比数列,故an=
|
(2)∵
| n |
 |
| i=1 |
=1+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
=
1(1-(
| ||
1-
|
| 1 |
| 2n |
点评:本题主要考查等差数列的定义和性质,等比数列的通项公式,递推数列的关系,等比数列前n项和,属于中档题.

练习册系列答案
相关题目
已知命题P:?x∈R,x2+2ax+a≤0.若命题P是假命题,则实数a的取值范围是( )
| A、(0,1) |
| B、(-∞,0)∪(1,+∞) |
| C、[0,1] |
| D、(-∞,0)∪[1,+∞) |

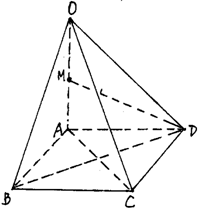 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.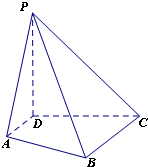 在四棱锥P-ABCD中,PD⊥平面ABCD,PD=CD=BC=2AD,AD∥BC,∠BCD=90°.
在四棱锥P-ABCD中,PD⊥平面ABCD,PD=CD=BC=2AD,AD∥BC,∠BCD=90°.