题目内容
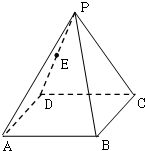 如图,在各棱长都相等且底面为正方形的四棱锥P-ABCD中,E为PD的中点.
如图,在各棱长都相等且底面为正方形的四棱锥P-ABCD中,E为PD的中点.(1)画出过A、E两点且与直线DC平行的平面与四棱锥的截面,并证明你的画法是正确的;
(2)若(1)中截面与PC交于点F,求异面直线DC与AF所成角的大小.
考点:直线与平面平行的性质,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)取PC中点F,则过A、E两点且与直线DC平行的平面为平面AEFB,四棱锥的截面为P-ABEF.
(2)由DC∥AB,知∠BAF就是异面直线DC与AF所成角,由已知条件,结合勾股定理能求出异面直线DC与AF所成角的大小.
(2)由DC∥AB,知∠BAF就是异面直线DC与AF所成角,由已知条件,结合勾股定理能求出异面直线DC与AF所成角的大小.
解答:
解:(1)取PC中点F,连结AE,EF,BF,
则过A、E两点且与直线DC平行的平面为平面AEFB,
四棱锥的截面为P-ABEF.
∵E是PD的中点,F是PC的中点,
∴EF∥DC,
∵CD不包含于平面AEFB,EF?平面AEFB,
∴DC∥平面AEFB.
(2)设四棱锥的棱长为a,
∵四棱锥P-ABCD中,各棱长都相等且底面为正方形,E为PD的中点,
∴AC=
=
a,BF=
=
a,
∵PA=PC=a,∴PA2+PC2=AC2,
∴∠APC=90°,∴AF=
=
a,
∴cos∠BAF=
=
=
,
∵DC∥AB,∴∠BAF就是异面直线DC与AF所成角,
∴异面直线DC与AF所成角为arccos
.
则过A、E两点且与直线DC平行的平面为平面AEFB,

四棱锥的截面为P-ABEF.
∵E是PD的中点,F是PC的中点,
∴EF∥DC,
∵CD不包含于平面AEFB,EF?平面AEFB,
∴DC∥平面AEFB.
(2)设四棱锥的棱长为a,
∵四棱锥P-ABCD中,各棱长都相等且底面为正方形,E为PD的中点,
∴AC=
| a2+a2 |
| 2 |
a2-(
|
| ||
| 2 |
∵PA=PC=a,∴PA2+PC2=AC2,
∴∠APC=90°,∴AF=
a2+(
|
| ||
| 2 |
∴cos∠BAF=
| AF2+AB2-BF2 |
| 2AF•AB |
=
| ||||
|
=
3
| ||
| 10 |
∵DC∥AB,∴∠BAF就是异面直线DC与AF所成角,
∴异面直线DC与AF所成角为arccos
3
| ||
| 10 |
点评:本题考查截面的作法及证明,考查异面直线所成角的大小的求法,解题时要注意空间思维能力的培养,是中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
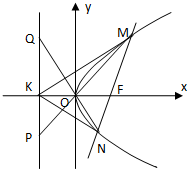 如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.
如图,已知抛物线y2=4x的焦点为F,过F的直线交抛物线于M、N两点,其准线l与x轴交于K点.