题目内容
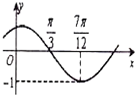函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，从而得到函数f（x）的解析式．再根据y=Asin（ωx+φ）的图象变换规律得出结论．
解答：
解：由函数f（x）=Asin（ωx+φ）的图象可得 A=1，
×
=
-
，解得ω=2．
再由五点法作图可得 2×
+φ=π，解得 φ=
，
故函数f（x）=sin（2x+
）=sin2（x+
），
故把g（x）=sin2x的图象向左平移
个长度单位可得f（x）的图象，
故选：C．
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
再由五点法作图可得 2×
| π |
| 3 |
| π |
| 3 |
故函数f（x）=sin（2x+
| π |
| 3 |
| π |
| 6 |
故把g（x）=sin2x的图象向左平移
| π |
| 6 |
故选：C．
点评：主要考查由函数y=Asin（ωx+∅）的部分图象求解析式，由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，y=Asin（ωx+∅）的图象变换规律，属于中档题．
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
对任意的实数x都有2x+4≥0的否定是（ ）
| A、对任意的实数x，都有2x+4≤0的否定 |
| B、存在实数x，满足2x+4≤0 |
| C、对任意的实数x，都有2x+4＜0的否定 |
| D、存在实数x，满足2x+4＜0 |
设等比数列{an}的首项为a1，公比为q，则{an}单调递减的充要条件是（ ）
| A、|q|＜1，且q≠0 |
| B、a1＞0，0＜q＜1 |
| C、a1＜0，q＞1 |
| D、a1＞0，0＜q＜1或a1＜0，q＞1 |
若非整实数x、y、z满足：2x=3y=6z．则．
A、
| ||
B、
| ||
C、
| ||
D、
|