题目内容
设等比数列{an}的首项为a1,公比为q,则{an}单调递减的充要条件是( )
| A、|q|<1,且q≠0 |
| B、a1>0,0<q<1 |
| C、a1<0,q>1 |
| D、a1>0,0<q<1或a1<0,q>1 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:由等比数列的通项公式表示出an,由指数函数的单调性进行判断即可.
解答:
解:由题意得,等比数列{an}的首项为a1,公比为q,
所以an=a1qn-1,由指数函数的单调性得,
当a1>0时,若0<q<1,则an=a1qn-1单调递减,
当a1<0时,若q>1,则an=a1qn-1单调递减,
反之也成立,a1>0,0<q<1或a1<0,q>1时,{an}单调递减,
综上得,{an}单调递减的充要条件是:a1>0,0<q<1或a1<0,q>1,
故选:D.
所以an=a1qn-1,由指数函数的单调性得,
当a1>0时,若0<q<1,则an=a1qn-1单调递减,
当a1<0时,若q>1,则an=a1qn-1单调递减,
反之也成立,a1>0,0<q<1或a1<0,q>1时,{an}单调递减,
综上得,{an}单调递减的充要条件是:a1>0,0<q<1或a1<0,q>1,
故选:D.
点评:本题考查等比数列的通项公式,指数函数的单调性,以及数列的函数特性,属于中档题.

练习册系列答案
相关题目
设f(x)=
,则f(2015)=( )
|
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
若函数f(x)=(x2+mx+n)(1-x2)的图象关于直线x=2对称,则f(x)的最大值是( )
| A、16 | B、14 | C、15 | D、18 |
阅读如图所示的程序框图,则该算法的功能是( )
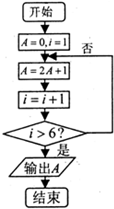

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前5项的和 |
| C、计算数列{2n-1}前6项的和 |
| D、计算数列{2n-1}前6项的和 |
已知函数f(x)=x2(x+3),若f′(x)=0,则( )
| A、x=0 | ||
| B、x=0或x=-2 | ||
C、x=-
| ||
| D、x=-2 |
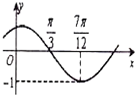 函数f(x)=sin(ωx+φ)(ω>0,|φ|<
函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|