题目内容
计算sin59°cos14°-sin14°cos59°= ．
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：逆用两角差的正弦，可得sin59°cos14°-sin14°cos59°=sin45°，于是可得答案．
解答：
解：sin59°cos14°-sin14°cos59°
=sin（59°-14°）
=sin45°=
．
故答案为：
．
=sin（59°-14°）
=sin45°=
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题考查两角差的正弦，逆用两角差的正弦，得到sin59°cos14°-sin14°cos59°=sin45°是关键，属于基础题．
练习册系列答案
相关题目
设函数f（x）=Asin（ωx+φ），（A≠0．ω＞0，|φ|＜
）的图象关于直线x=
对称，它的周期是π，则（ ）
| π |
| 2 |
| 2π |
| 3 |
A、f（x）的图象过点（0，
| ||||
B、f（x）在[
| ||||
C、f（x）的一个对称点中心是（
| ||||
| D、f（x）的最大值是A |
若不论k为何值，直线y=k（x-2）+b与曲线x2+y2=9总有公共点，则b的取值范围是（ ）
| A、（-2，2） | ||||
| B、[-2，2] | ||||
C、（-
| ||||
D、[-
|
下列说法错误的是（ ）
| A、命题“?x∈R，x2-2x=0”的否定是“?x∈R，x2-2x≠0” |
| B、命题“若m＞0，则方程x2+x-m=0有实根”的逆否命题为真命题 |
| C、若命题“p∧q”为真命题，则“p∨q”为真命题 |
| D、“x＞1”是“|x|＞0”的必要不充分条件 |
椭圆x2+3y2=6的焦距为（ ）
| A、1 | B、2 | C、3 | D、4 |
设f（x）=
，则f（2015）=（ ）
|
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
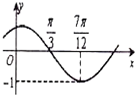函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|