题目内容
11.已知(a+e)x-1-lnx≤0(e是自然对数的底数)对任意x∈[$\frac{1}{e}$,2]都成立,则实数a的最大值为-e.分析 问题转化为a( $\frac{1+lnx}{x}$-e)min对于任意x∈[$\frac{1}{e}$,2]恒成立,设f(x)=$\frac{1+lnx}{x}$-e,求出函数f(x)的最小值即可求出a的最大值.
解答 解:(a+e)x-1-lnx≤0对于任意x∈[$\frac{1}{e}$,2]恒成立
?a≤$\frac{1+lnx}{x}$-e对于任意x∈[$\frac{1}{e}$,2]恒成立
?a≤( $\frac{1+lnx}{x}$-e)min对于任意x∈[$\frac{1}{e}$,2]恒成立
设f(x)=$\frac{1+lnx}{x}$-e,x∈[$\frac{1}{e}$,2],则f′(x)=-$\frac{lnx}{{x}^{2}}$,
令f′(x)>0,解得:$\frac{1}{e}$≤x<1,令f′(x)>0,解得:1<x≤2,
∴f(x)在[$\frac{1}{e}$,1)递增,在(1,2]递减,
∴f($\frac{1}{e}$)或f(2)最小,
而f($\frac{1}{e}$)=-e,f(2)=$\frac{1}{2}$(1+ln2)-e,
∴f($\frac{1}{e}$)<f(2),
∴a的最大值是-e,
故答案为:-e.
点评 本题考查函数恒成立问题,着重考查构造函数思想、等价转化思想与导数法求极值的综合应用,求得f(x)的最小值是关键,属于中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
6.在调查480名男人中有38名患有色盲,520名女人中有6名患有色盲,根据调查数据作出如下的列联表:
利用独立性检验的方法来判断色盲与性别有关?你所得到的结论在什么范围内有效?
注:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(χ2≥10.828)≈0.001,P(χ2≥5.024)≈0.025,P(χ2≥6.635)≈0.01.
| 色盲 | 不色盲 | 合计 | |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 合计 | 44 | 956 | 1000 |
注:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(χ2≥10.828)≈0.001,P(χ2≥5.024)≈0.025,P(χ2≥6.635)≈0.01.
16. 观察如图,则第( )行的各数之和等于20152.
观察如图,则第( )行的各数之和等于20152.
 观察如图,则第( )行的各数之和等于20152.
观察如图,则第( )行的各数之和等于20152.| A. | 2014 | B. | 2016 | C. | 1007 | D. | 1008 |
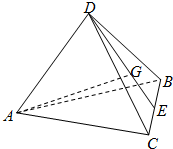 如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.
如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$. 图中的三个正方形块中,着色的正方形的个数依次构成一个数列{an},根据着色的规律,则a4=585,数列{an}的通项公式an=$\frac{{8}^{n}-1}{7}$.
图中的三个正方形块中,着色的正方形的个数依次构成一个数列{an},根据着色的规律,则a4=585,数列{an}的通项公式an=$\frac{{8}^{n}-1}{7}$.