题目内容
1.已知直线l过直线3x+4y-5=0和2x+y=0的交点且与直线3x-2y-1=0垂直.(1)求l的方程;
(2)求直线l的横截距和纵截距.
分析 (1)由题意可知求得两直线的交点,由垂直于直线3x-2y-1=0的直线方程是:2x+3y+c=0,代入即可求得c的值,求得直线l的方程;
(2)分别令x=0,y=0,求出直线的横截距和纵截距即可.
解答 解:(1)设垂直于直线3x-2y-1=0的直线方程是:2x+3y+c=0,
设直线l过直线3x+4y-5=0和2x+y=0的交点P(x,y);
由$\left\{\begin{array}{l}{3x+4y-5=0}\\{2x+y=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$,
P(-1,2),
代入2x+3y+c=0得:-2+6+c=0,
解得:c=-4,
∴直线l:2x+3y-4=0;
(2)由(1)x=0时,y=$\frac{4}{3}$,纵截距是$\frac{4}{3}$;
y=0时,x=2,横截距是2.
点评 本题考查求直线的交点坐标的方法,考查与直线垂直的直线方程的求法,考查计算能力,属于中档题.

练习册系列答案
相关题目
12.已知f(x)=$\left\{\begin{array}{l}{\frac{1}{x},1≤x≤2}\\{{e}^{-x},0≤x≤1}\end{array}\right.$,则${∫}_{0}^{2}$f(x)dx=( )
| A. | $\frac{1}{e}$+ln2 | B. | -$\frac{1}{e}$+ln2 | C. | 1-$\frac{1}{e}$+ln2 | D. | $\frac{1}{e}$+ln2-1 |
10.已知某三角函数的部分图象如图所示,则它的解析式可能是( )
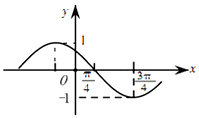

| A. | $y=sin(x+\frac{π}{4})$ | B. | $y=sin(2x+\frac{3π}{4})$ | C. | $y=cos(x+\frac{π}{4})$ | D. | $y=cos(2x+\frac{3π}{4})$ |