题目内容
1.已知函数f(x)=$\frac{{x}^{3}}{3}$+$\frac{m{x}^{2}+(m+n)x+1}{2}$(x∈R),且f(x)有两个极值点x1,x2,满足x1∈(0,1),x2∈(1,+∞),点P(m,n)在平面直角坐标系中表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围是(1,3).分析 求出函数的导数,得到关于m,n的不等式组,画出满足条件的平面区域,结合图象求出a的范围即可.
解答 解:求导函数可得f'(x)=x2+mx+$\frac{1}{2}$(m+n),
依题意知,方程f'(x)=0有两个根x1、x2,且x1∈(0,1),x2∈(1,+∞),
构造函数f(x)=x2+mx+$\frac{1}{2}$(m+n),
∴$\left\{\begin{array}{l}{f(0)>0}\\{f(1)<0}\end{array}\right.$,∴$\left\{\begin{array}{l}{m+n>0}\\{2+3m+n<0}\end{array}\right.$,
如图示: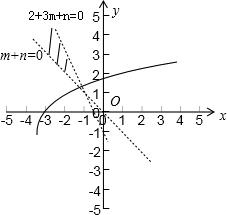
∵直线m+n=0,2+3m+n=0的交点坐标为(-1,1)
∴要使函数y=loga(x+4)(a>1)的图象上存在区域D上的点,
则必须满足1<loga(-1+4)
∴loga3<1,解得a<3
又∵a>1,
∴1<a<3,
故答案为:(1,3).
点评 本题考查了线性规划问题,考查导数的应用以及对数函数的性质,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.中国柳州从2011年起每年国庆期间都举办一届国际水上狂欢节,到2016年已举办了六届,旅游部门统计在每届水上狂欢节期间,吸引了不少外地游客到柳州,这将极大地推进柳州的旅游业的发展,现将前五届水上狂欢节期间外地游客到柳州的人数统计表如表:
(1)求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)旅游部门统计在每届水上狂欢节期间,每位外地游客可为本市增加100元左右的旅游收入,利用(1)中的线性回归方程,预测2017年第7届柳州国际水上狂欢节期间外地游客可为本市增加的旅游收入达多少?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
| 份(x) | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 水上狂欢节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
(2)旅游部门统计在每届水上狂欢节期间,每位外地游客可为本市增加100元左右的旅游收入,利用(1)中的线性回归方程,预测2017年第7届柳州国际水上狂欢节期间外地游客可为本市增加的旅游收入达多少?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
1.若复数z满足(1-z)(1+2i)=i,则在复平面内表示复数z的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
9.若实数x,y满足{x≥0y≥04x+3y≤12,则z=y+12x-2的取值范围是( )
| A. | [-12,14] | B. | [-52,14] | C. | (-∞,-12]∪[14,+∞) | D. | (-∞,-52]∪[14,+∞) |
6.在一个锐二面角的一个面内有一点,它到棱的距离等于到另一个平面的距离的2倍,则二面角大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |