题目内容
19.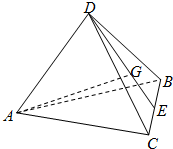 如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.
如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.
分析 由已知求解直角三角形可得DE、AE的长,由余弦定理求得cos∠ADG,在△ADG中,再由余弦定理求得AG.
解答 解:∵AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,
∴BC=$\sqrt{5}$,DB=$\sqrt{9+1-2×3×1×cos60°}$=$\sqrt{9+1-2×3×1×\frac{1}{2}}=\sqrt{7}$,
DC=$\sqrt{9+4-2×3×2×cos60°}$=$\sqrt{9+4-2×3×2×\frac{1}{2}}=\sqrt{7}$,
∴DE=$\sqrt{(\sqrt{7})^{2}-(\frac{\sqrt{5}}{2})^{2}}=\frac{\sqrt{23}}{2}$,AE=$\frac{\sqrt{5}}{2}$,
在△ADE中,有cos∠ADG=$\frac{9+(\frac{\sqrt{23}}{2})^{2}-\frac{5}{4}}{2×3×\frac{\sqrt{23}}{2}}=\frac{9\sqrt{23}}{46}$,
∵DG=2GE,∴DG=$\frac{\sqrt{23}}{3}$,
∴在△ADG中,AG=$\sqrt{9+\frac{23}{9}-2×3×\frac{\sqrt{23}}{3}×\frac{9\sqrt{23}}{46}}=\frac{\sqrt{23}}{3}$.
故答案为:$\frac{{\sqrt{23}}}{3}$.
点评 本题考查空间距离的计算,考查余弦定理的运用,考查学生的计算能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若实数x,y满足{x≥0y≥04x+3y≤12,则z=y+12x-2的取值范围是( )
| A. | [-12,14] | B. | [-52,14] | C. | (-∞,-12]∪[14,+∞) | D. | (-∞,-52]∪[14,+∞) |
7.直线xcosθ+ysinθ+a=0与圆x2+y2=a2交点的个数是( )
| A. | 0 | B. | 1 | C. | 随a变化 | D. | 随θ变化 |
14.函数y=x3-3x2-9x(0<x<4)有( )
| A. | 极大值5,极小值-27 | B. | 极大值5,极小值-11 | ||
| C. | 极大值5,无极小值 | D. | 极小值-27,无极大值 |
8.与⊙C1:x2+(y+2)2=25内切且与⊙C2:x2+(y-2)2=1外切的动圆圆心M的轨迹方程是( )
| A. | $\frac{x^2}{9}$+$\frac{y^2}{5}$=1(y≠0) | B. | $\frac{y^2}{9}$+$\frac{x^2}{5}$=1(x≠0) | C. | $\frac{x^2}{9}$+$\frac{y^2}{5}$=1(x≠3) | D. | $\frac{y^2}{9}$+$\frac{x^2}{5}$=1(y≠3) |