题目内容
等差数列{an}中,若a3+a4+a5+a6+a7=450,则前9项和S9=( )
| A、1620 | B、810 |
| C、900 | D、675 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:由 a3+a4+a5+a6+a7=450,及等差数列的性质 可得5a5=450,a5=90,据前9项和S9=
(a1+a9)=9a5 求出结果.
| 9 |
| 2 |
解答:
解:∵在等差数列{an}中,a3+a4+a5+a6+a7=450,
∴5a5=450,a5=90.
∴前9项和S9=
(a1+a9)=9a5=810,
故选:B.
∴5a5=450,a5=90.
∴前9项和S9=
| 9 |
| 2 |
故选:B.
点评:本题考查等差数列的定义和性质,前n项和公式的应用,求出a5=90,是解题的关键.

练习册系列答案
相关题目
设数列{an}是等差数列,其前n项和为Sn,若a6=2,S5=30,则S8=( )
| A、31 | B、32 | C、33 | D、34 |
设正项等差数列{an}的前n项和为Sn,若S2012=2012,则
+
的最小值为( )
| 1 |
| a1 |
| 1 |
| a2012 |
| A、1 | B、2 | C、4 | D、8 |
已知定点A(1,2)和直线l:x+2y-5=0,那么到定点A的距离和到定直线l距离相等的点的轨迹为( )
| A、椭圆 | B、双曲线 |
| C、抛物线 | D、直线 |
对于任意实数a、b、c、d,下列命题:
①若a>b,c≠0,则ac>bc;
②若a>b,则ac2>bc2;
③若ac2>bc2,则a>b;
④若a>b,则
<
中.
真命题个数为( )
①若a>b,c≠0,则ac>bc;
②若a>b,则ac2>bc2;
③若ac2>bc2,则a>b;
④若a>b,则
| 1 |
| a |
| 1 |
| b |
真命题个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知P=(x2+1)2,Q=x4+x2+1,那么P,Q的大小关系是( )
| A、P≥Q | B、P<Q |
| C、P≤Q | D、无法确定 |
图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得.现用一个竖直的平面去截这个几何体,则截面图形可能是( )

| A、(1)(2) |
| B、(1)(3) |
| C、(1)(4) |
| D、(1)(5) |
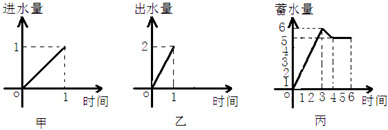 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:
一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断: