题目内容
16.已知F是椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左焦点,设动点P在椭圆上,若直线FP的斜率大于$\sqrt{3}$,则直线OP(O为原点)的斜率的取值范围是( )| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{2}}]∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}}]$ | C. | $({-∞,-\frac{3}{2}})∪({\frac{{3\sqrt{3}}}{8},\frac{3}{2}})$ | D. | $[{-\frac{3}{2},+∞})$ |
分析 由题意画出图形,得到满足直线FP的斜率大于$\sqrt{3}$的P的范围,则直线OP的斜率的取值范围可求.
解答 解:由$\frac{x^2}{4}+\frac{y^2}{3}=1$,得a2=4,b2=3,∴$c=\sqrt{{a}^{2}-{b}^{2}}=1$.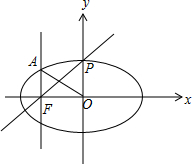
则F(-1,0),
如图:过F作垂直于x轴的直线,交椭圆于A(x轴上方),则xA=-1,
代入椭圆方程可得${y}_{A}=\frac{3}{2}$.
当P为椭圆上顶点时,P(0,$\sqrt{3}$),此时${k}_{FP}=\sqrt{3}$,
又${k}_{OA}=-\frac{3}{2}$,
∴当直线FP的斜率大于$\sqrt{3}$时,直线OP的斜率的取值范围是$(-∞,-\frac{3}{2})$.
故选:A.
点评 本题考查椭圆的简单性质,考查数形结合的解题思想方法,是基础题.

练习册系列答案
相关题目
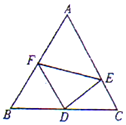 如图,在边长为2的正三角形△ABC中,D为BC的中点,E,F分别在边CA,AB上.
如图,在边长为2的正三角形△ABC中,D为BC的中点,E,F分别在边CA,AB上.