题目内容
设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn,则log2013x1+log2013x2+…+log2013x2012的值为 .
考点:利用导数研究曲线上某点切线方程,对数的运算性质
专题:导数的综合应用
分析:由导数求出函数在点(1,1)处的切线方程,得到切线在x轴上的截距,然后利用对数的运算性质化简
log2013x1+log2013x2+…+log2013x2012,把数列{xn}累积后代入得答案.
log2013x1+log2013x2+…+log2013x2012,把数列{xn}累积后代入得答案.
解答:
解:由y=xn+1,得y′=(n+1)xn,
∴y′|x=1=n+1,
则曲线y=xn+1(n∈N*)在点(1,1)处的切线方程为y-1=(n+1)(x-1),
取y=0得:x=
.
则log2013x1+log2013x2+…+log2013x2012
=log2013(x1x2…x2012)=log2013(
•
…
)=log2013
=-1.
故答案为:-1.
∴y′|x=1=n+1,
则曲线y=xn+1(n∈N*)在点(1,1)处的切线方程为y-1=(n+1)(x-1),
取y=0得:x=
| n |
| n+1 |
则log2013x1+log2013x2+…+log2013x2012
=log2013(x1x2…x2012)=log2013(
| 1 |
| 2 |
| 2 |
| 3 |
| 2012 |
| 2013 |
| 1 |
| 2013 |
故答案为:-1.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了对数的运算性质,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知二项式(
-
)7展开式的第4项与第5项之和为零,那么x等于( )
| x |
| 2 | ||
|
| A、1 | ||
B、
| ||
| C、2 | ||
| D、46 |
设函数f1(x)=log4x-(
)x、f2(x)=log
x-(
)x的零点分别为x1、x2,则( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、x1x2≥2 |
| B、1<x1x2<2 |
| C、x1x2=1 |
| D、0<x1x2<1 |
 如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )| A、64 | B、63 | C、62 | D、61 |
某几何体的三视图如图所示,它的体积为( )
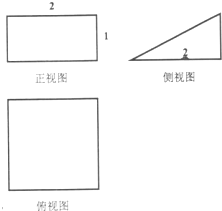

| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
设随机变量X~N(1,52),且P(X≤0)=P(X>a-2),则实数a的值为( )
| A、4 | B、6 | C、8 | D、10 |