题目内容
设函数f1(x)=log4x-(
)x、f2(x)=log
x-(
)x的零点分别为x1、x2,则( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、x1x2≥2 |
| B、1<x1x2<2 |
| C、x1x2=1 |
| D、0<x1x2<1 |
考点:函数的零点
专题:函数的性质及应用
分析:由题意可得x1是函数y=log4x的图象和y=(
)x的图象的交点的横坐标,x2是y=log
x的图象和函数y=(
)x的图象的交点的横坐标,根据log
x2>log4x1,求得0<x1•x2<1,从而得出结论.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
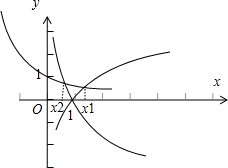 解:由题意可得x1是函数y=log4x的图象和y=(
解:由题意可得x1是函数y=log4x的图象和y=(
)x的图象的交点的横坐标,
x2是y=log
x的图象和函数y=y=(
)x的图象的交点的横坐标,且x1,x2都是正实数,如图所示:
故有log
x2>log4x1,故 log4x1-log
x2<0,
∴log4x1+log4x2<0,
∴log4(x1•x2)<0,
∴0<x1•x2<1,
故选:D.
 解:由题意可得x1是函数y=log4x的图象和y=(
解:由题意可得x1是函数y=log4x的图象和y=(| 1 |
| 4 |
x2是y=log
| 1 |
| 4 |
| 1 |
| 4 |
故有log
| 1 |
| 4 |
| 1 |
| 4 |
∴log4x1+log4x2<0,
∴log4(x1•x2)<0,
∴0<x1•x2<1,
故选:D.
点评:本题主要考查对数函数、指数函数的图象和性质应用,体现了数形结合和转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈({0,
),不等式f(x)+2<1ogax恒成立时,实数a的取值范围是( )
| 1 |
| 2 |
A、(
| |||||
B、[
| |||||
C、(
| |||||
D、[
|
 如图,在平面直角坐标系中,正方形OABC的边长为1,E为AB的中点,若F为正方形内(含边界)任意一点,则
如图,在平面直角坐标系中,正方形OABC的边长为1,E为AB的中点,若F为正方形内(含边界)任意一点,则