题目内容
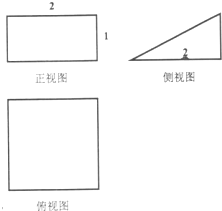
某几何体的三视图如图所示,它的体积为( )

| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可得,该几何体为三棱柱,求出底面面积和高,代入三棱柱体积公式,可得答案.
解答:
解:由已知中的三视图可得,该几何体为以侧视图为底面的三棱柱,
棱柱的底面面积S=
×2×1=1,
棱柱的高h=2,
故棱柱的体积V=Sh=2,
故选:A
棱柱的底面面积S=
| 1 |
| 2 |
棱柱的高h=2,
故棱柱的体积V=Sh=2,
故选:A
点评:本题考查三视图、三棱柱的体积,本试题考查了简单几何体的三视图的运用.培养同学们的空间想象能力和基本的运算能力.基础题.

练习册系列答案
相关题目
若函数f(x)=|ax+x2-xlna-t|-1(a>1)有三个零点,则t的值是( )
| A、2 | B、4 | C、8 | D、0 |
已知函数f(x)对于一切实数x,y均有f(x+y)-f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈({0,
),不等式f(x)+2<1ogax恒成立时,实数a的取值范围是( )
| 1 |
| 2 |
A、(
| |||||
B、[
| |||||
C、(
| |||||
D、[
|
曲线y=-3x3+2在点(0,2)处的切线的斜率是( )
| A、-6 | B、6 | C、0 | D、不存在 |
下列判断错误的是( )
| A、“am2<bm2”是“a<b”的充分不必要条件 |
| B、命题“对任意x∈R,x3-x2-1≤0”的否定是“存在x0∈R,x03-x02-1>0” |
| C、若X~B(4,0.25)则DX=0.75 |
| D、若p或q为假命题,则p、q均为假命题 |
