题目内容
已知sin10°=k，则cos620°等于（ ）
| A、k | ||
| B、-k | ||
| C、±k | ||
D、
|
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：运用同角三角函数基本关系化简即可求值．
解答：
解：∵sin10°=k，
∴cos620°=cos（360°+260°）=cos260°=cos（180°+90°-10°）=-cos（90°-10°）=-sin10°=-k．
故选：B．
∴cos620°=cos（360°+260°）=cos260°=cos（180°+90°-10°）=-cos（90°-10°）=-sin10°=-k．
故选：B．
点评：本题主要考察了同角三角函数基本关系的运用，诱导公式的应用，属于基本知识的考查．
练习册系列答案
相关题目
已知在△ABC中，a=8，∠A=45°，∠B=60°，则b=（ ）
A、4
| ||
B、4
| ||
C、4
| ||
D、
|
若非直角△ABC的内角A、B、C成等差数列，则tanA+tanC-tanAtanBtanC=（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
已知
=（1，-
，
），
=（-3，λ，-
）满足
∥
，则λ等于（ ）
| a |
| 3 |
| 2 |
| 5 |
| 2 |
| b |
| 15 |
| 2 |
| a |
| b |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设偶函数f（x）的定义域为R，当x∈[0，+∞）时，f（x）是减函数，则f（-2），f（π），f（-1）的大小关系是（ ）
| A、f（-2）＜f（-1）＜f（π） |
| B、f（-2）＜f（π）＜f（-1） |
| C、f（-2）＞f（π）＞f（-1） |
| D、f（-1）＞f（-2）＞f（π） |
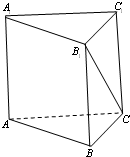如图，正三棱柱的底面边长为1，体积为