Question

定义在（0，+∞）上的函数f（x）满足：①当x∈[1，3）时，f（x）=1-|x-2|；②f（3x）=3f（x）．设关于x的函数F（x）=f（x）-a的零点从小到大依次为x₁，x₂，…，x_n，…．若a∈（1，3），则x₁+x₂+…+x₂₀₁₄=

 

．

Answer 1

考点：函数零点的判定定理

专题：函数的性质及应用

分析：利用已知可得：当x∈[3，6]时，由

x

3

∈[1，2]，可得f（x）=3f（

x

3

），f（x）∈[0，3]；同理，当x∈（6，9）时，f（x）∈[0，3]；此时f（x）∈[0，3]．分别作出y=f（x），y=a，则F（x）=f（x）-a在区间（3，6）和（6，9）上各有一个零点，分别为x₁，x₂，且满足x₁+x₂=2×6，依此类推：x₃+x₄=2×18，…，x₂₀₁₃+x₂₀₁₄=2×2×3¹⁰⁰⁷．利用等比数列的前n项和公式即可得出．

解答： 解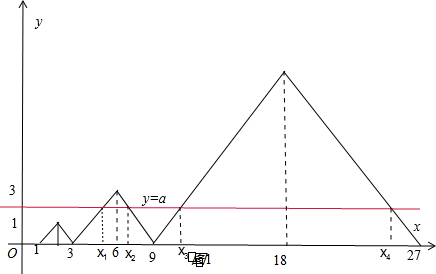：∵①当x∈[1，3）时，f（x）=1-|x-2|∈[0，1]；②f（3x）=3f（x）．
∴当

1

3

≤x＜时，则1≤3x＜3，由f（x）=

1

3

f（3x）可知：f（x）∈[0，

1

3

]．
同理，当x∈（0，

1

3

）时，0≤f（x）＜1，
当x∈[3，6]时，由

x

3

∈[1，2]，可得f（x）=3f（

x

3

），f（x）∈[0，3]；
同理，当x∈（6，9）时，由

x

3

∈（2，3），可得f（x）=3f（

x

3

），f（x）∈[0，3]；
此时f（x）∈[0，3]．
当a∈（1，3）时．
则F（x）=f（x）-a在区间（3，6）和（6，9）上各有一个零点，分别为x₁，x₂，且满足x₁+x₂=2×6，
依此类推：x₃+x₄=2×18，…，x_2n-1+x_2n=2×2×3ⁿ．
∴当a∈（1，3）时，x₁+x₂+…+x₂₀₁₃+x₂₀₁₄=4×（3+3²+…+3¹⁰⁰⁷）=4×3×

31007-1

3-1

=6×（3¹⁰⁰⁷-1），
故答案为：6×（3¹⁰⁰⁷-1）．

点评：本题考查了函数的图象与性质、区间转换、对称性、等比数列的前n项和公式等基础知识与基本技能，属于难题．