题目内容
已知函数f(x)=
（1）求f（3）的值；
（2）用单调性定义证明函数f（x）在（-∞，+∞）上是增函数．
| 2x-1 |
| 2x+1 |
（1）求f（3）的值；
（2）用单调性定义证明函数f（x）在（-∞，+∞）上是增函数．
考点：函数单调性的判断与证明,函数的值
专题：计算题,证明题,函数的性质及应用
分析：（1）代入求值即可，
（2）用定义法证明单调性一般可以分为五步，取值，作差，化简变形，判号，下结论．
（2）用定义法证明单调性一般可以分为五步，取值，作差，化简变形，判号，下结论．
解答：
解：（1）f(3)=
=
；
（2）任取x1，x2∈（-∞，+∞），且x1＜x2，
则f(x1)-f(x2)=
-
=
=
，
∵x1＜x2∴2x1＜2x2，
即 2x1-2x2＜0，
又∵2x1+1＞0，2x2+1＞0，
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2），
∴函数f（x）在（-∞，+∞）上是增函数．
| 23-1 |
| 23+1 |
| 7 |
| 9 |
（2）任取x1，x2∈（-∞，+∞），且x1＜x2，
则f(x1)-f(x2)=
| 2x1-1 |
| 2x1+1 |
| 2x2-1 |
| 2x2+1 |
=
| (2x1-1)(2x2+1)-(2x2-1)(2x1+1) |
| (2x1+1)(2x2+1) |
=
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
∵x1＜x2∴2x1＜2x2，
即 2x1-2x2＜0，
又∵2x1+1＞0，2x2+1＞0，
∴f（x1）-f（x2）＜0，
即f（x1）＜f（x2），
∴函数f（x）在（-∞，+∞）上是增函数．
点评：本题主要考查了函数单调性的证明，一般有两种方法，定义法，导数法．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
若点O是△ABC的外心，且
+
+
=
，则△ABC的内角C为（ ）
| OA |
| OB |
| CO |
| 0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
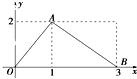函数f（x）的图象是如下图所示的折线段OAB，点A的坐标为（1，2），点B的坐标为（3，0）