题目内容
设数列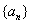 的各项均为正数,前
的各项均为正数,前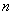 项和为
项和为 ,已知
,已知 .
.
(1)证明数列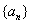 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)证明:对任意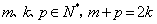 ,都有
,都有 ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由.
(1)∵ ,∴当
,∴当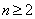 时,
时,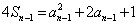 .
.
两式相减得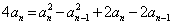 ,∴
,∴
∵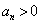 ,∴
,∴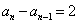 ,又
,又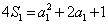 ,∴
,∴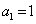
∴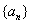 是以
是以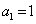 为首项,
为首项,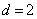 为公差的等差数列.∴
为公差的等差数列.∴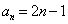
(2)由(1)知 ,∴
,∴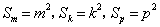
于是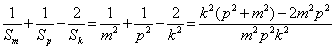
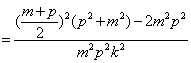
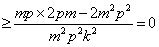
∴
(3)结论成立,证明如下:
设等差 数列
数列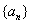 的首项为
的首项为 ,公差为
,公差为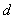 ,则
,则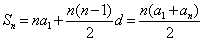
于是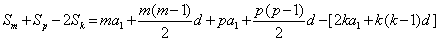

将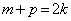 代入得,
代入得, ,∴
,∴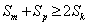
又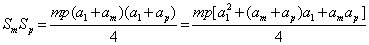
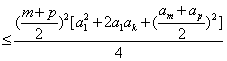
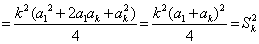
∴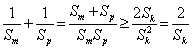 .
.

练习册系列答案
相关题目
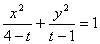 表示曲线C,给出以下命题:
表示曲线C,给出以下命题: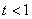 或
或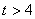 ;
; ,则曲线C为椭圆; ④若曲线C为焦点在x轴上的椭圆,则1<t<
,则曲线C为椭圆; ④若曲线C为焦点在x轴上的椭圆,则1<t<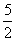 .
.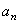 =__________________.
=__________________.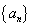 满足
满足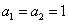 ,
,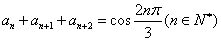 ,若数列
,若数列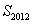 的值为( )
的值为( )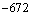 B.
B.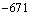 C.
C. D.
D.
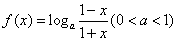 .
.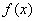 的定义域
的定义域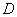 ,并判断
,并判断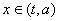 时,
时,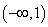 ,求
,求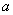 与
与 的值;
的值;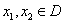 ,是否存在
,是否存在 ,使得
,使得 ,若存在,求出
,若存在,求出 ;若不存在,请说明理由.
;若不存在,请说明理由.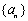 是无穷等比数列,其前n项和是
是无穷等比数列,其前n项和是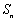 ,若
,若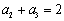 ,
, 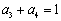 ,则
,则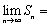 .
.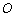 为
为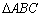 的外心,
的外心,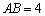 ,
,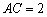 ,
,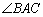 为钝角,
为钝角,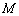 是边
是边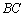 的中点,则
的中点,则
 的方程为
的方程为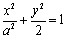
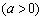 ,其焦点在
,其焦点在 轴上,点
轴上,点
 为椭圆上一点.
为椭圆上一点.
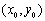 满足
满足 ,其中
,其中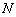 是椭圆
是椭圆 与
与
 ,求证:
,求证: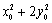 为定值;
为定值;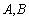 ,使得
,使得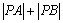 为定值?
为定值?  ,
, ,则
,则 .
.