题目内容
已知函数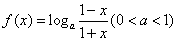 .
.
(1)求函数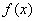 的定义域
的定义域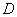 ,并判断
,并判断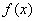 的奇偶性;
的奇偶性;
(2)如果当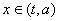 时,
时,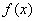 的值域是
的值域是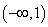 ,求
,求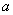 与
与 的值;
的值;
(3)对任意的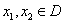 ,是否存在
,是否存在 ,使得
,使得 ,若存在,求出
,若存在,求出 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)令 ,解得
,解得 ,
,
对任意

所以函数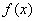 是奇函数.
是奇函数.
(2)由 知,函数
知,函数 在
在 上单调递减,
上单调递减,
因为 ,所以
,所以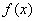 在
在 上是增函数
上是增函数
又因为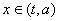 时,
时,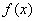 的值域是
的值域是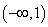 ,所以
,所以
且 在
在 的值域是
的值域是 ,
,
故 且
且 (结合
(结合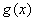 图像易得
图像易得 )
)
 解得
解得 (
( 舍去).所以
舍去).所以 ,
,
(3)假设存在 使得
使得
即

 ,解得
,解得 ,
,
下证: .
.
证明:
 ,∴
,∴ ,
,
∴ ,即
,即 ,∴
,∴
所以存在 ,使得
,使得

练习册系列答案
相关题目
 分别为双曲线
分别为双曲线 的左、右焦点.若在双曲线右支上存在点
的左、右焦点.若在双曲线右支上存在点 ,满足
,满足 ,且
,且 到直线
到直线 的距离等于双曲线的实轴长,则该双曲线的离心率为( )
的距离等于双曲线的实轴长,则该双曲线的离心率为( ) B.
B. C.
C. D.
D.
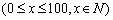 时,销售收入函数
时,销售收入函数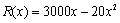 (单位:百元),其成本函数满足
(单位:百元),其成本函数满足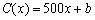 (单位:百元).已知该公司不生产任何产品时,其成本为4000(百元).
(单位:百元).已知该公司不生产任何产品时,其成本为4000(百元).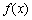 ,我们把函数
,我们把函数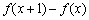 称为函数
称为函数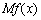 .对于(1)求得的利润函数
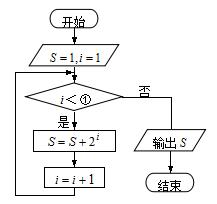
.对于(1)求得的利润函数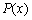 ,求边际函数
,求边际函数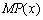 ;并利用边际函数
;并利用边际函数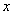 的值,输出相应的
的值,输出相应的 值.若要使输入的
值.若要使输入的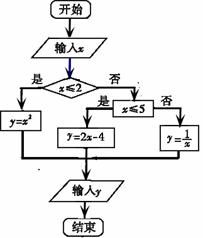
 数
数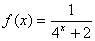 ,若函数
,若函数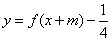 为奇函数,则实数
为奇函数,则实数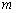 为( )
为( )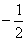 B.
B.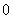 C.
C. 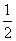 D.
D.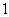
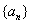 的各项均为正数,前
的各项均为正数,前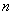 项和为
项和为 ,已知
,已知 .
.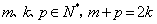 ,都有
,都有 ;
;
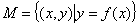 ,若对于任意
,若对于任意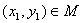 ,存在
,存在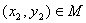 ,使得
,使得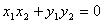 成立,则称集合
成立,则称集合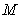 是“
是“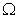 集合”. 给出下列4个集合:
集合”. 给出下列4个集合: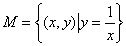 ②
② 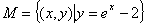
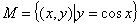 ④
④ 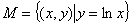
 ,
, ,则
,则 .
.