题目内容
已知椭圆 的方程为
的方程为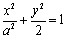
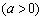 ,其焦点在
,其焦点在 轴上,点
轴上,点
 为椭圆上一点.
为椭圆上一点.
(1)求该椭圆的标准方程;
(2)设动点
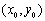 满足
满足 ,其中
,其中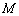 、
、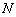 是椭圆
是椭圆 上的点,直线
上的点,直线 与
与
的斜率之积为 ,求证:
,求证: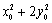 为定值;
为定值;
(3)在(2)的条件下探究:是否存在两个定点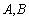 ,使得
,使得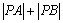 为定值?
为定值?
若存在,给出证明;若不存在,请说明理由.
(1)因为点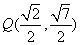 为椭圆上一点,所以
为椭圆上一点,所以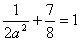 ,
,
得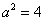 ,椭圆方程为
,椭圆方程为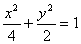
(2)设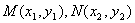 , 又
, 又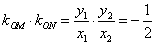 ,化简得
,化简得 2分
2分
则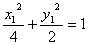 ,
,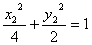 ,
,
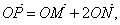
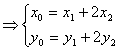
所以
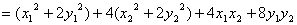
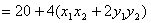
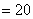 (定值)
(定值)
(3)因为动点P(x0,y0)满足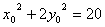 ,即
,即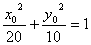 ,
,
所以点P的轨迹为焦点 的椭圆.
的椭圆.
存在点A(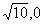 )、B(
)、B( ),使得
),使得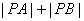 =
= (定值)
(定值)

练习册系列答案
相关题目
 三边的中点)得到的几何体如图2,则按图2所示方向侧视该几何体所呈现的平面图形为( )
三边的中点)得到的几何体如图2,则按图2所示方向侧视该几何体所呈现的平面图形为( )

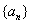 的各项均为正数,前
的各项均为正数,前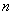 项和为
项和为 ,已知
,已知 .
.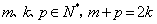 ,都有
,都有 ;
;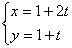 的倾斜角等于( )
的倾斜角等于( )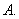

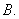
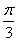
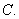
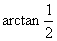
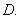
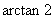
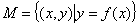 ,若对于任意
,若对于任意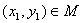 ,存在
,存在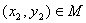 ,使得
,使得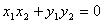 成立,则称集合
成立,则称集合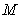 是“
是“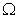 集合”. 给出下列4个集合:
集合”. 给出下列4个集合: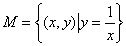 ②
② 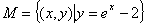
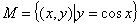 ④
④ 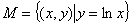
 的定义域为
的定义域为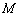 ,函数
,函数 的值域为
的值域为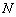 ,则
,则 .
. 的展开式中,第4项与第7项的二项式系数相等,则展开式中
的展开式中,第4项与第7项的二项式系数相等,则展开式中 的系数为 .(用数字作答)
的系数为 .(用数字作答) 平面
平面 ,矩形
,矩形 ,
, ,
,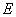 为
为 的中点.
的中点. ,求异面直线
,求异面直线 与
与 所成的角的大小.
所成的角的大小.
 为第二象限角,
为第二象限角, ,则
,则 ____________.
____________.