题目内容
3.[已知锐角三角形ABC中,角A,B,C所对边分别为a,b,c满足$\sqrt{\frac{1-cos2C}{2}}+sin(B-A)=2sin2A$.(Ⅰ)求$\frac{a}{b}$;
(Ⅱ)若AB是最大边,求cosC的取值范围.
分析 (Ⅰ)由条件利用二倍角的余弦公式,两角和差的三角公式,求得sinBcosA=2sinAcosA,再利用正弦定理求得$\frac{a}{b}$的值.
(Ⅱ)由条件利用余弦定理,求得cosC的取值范围.
解答 解:(Ⅰ)∵$\sqrt{\frac{1-cos2C}{2}}=sinC=sin(A+B)$,且 $\sqrt{\frac{1-cos2C}{2}}+sin(B-A)=2sin2A$,
∴sin(A+B)+sin(B-A)=2sin2A,∴sinBcosA=2sinAcosA,
因△ABC为锐角三角形,则cosA≠0,由正弦定理有:$\frac{a}{b}=\frac{sinA}{sinB}=\frac{1}{2}$.
(Ⅱ)∵b=2a,且a<b≤c,则$\frac{π}{3}<C<\frac{π}{2}$,即$0<cosC<\frac{1}{2}$,
又因$cosC=\frac{{{a^2}+{b^2}-{c^2}}}{2ab}≤\frac{a^2}{2ab}=\frac{1}{4}$,∴cosC的取值范围是$(0,\frac{1}{4}]$.
点评 本题主要考查二倍角的余弦公式,两角和差的三角公式,正弦定理和余弦定理的应用,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.已知双曲线C$:\frac{x^2}{a^2}-\frac{y^2}{4}=1$的一条渐近线方程为2x+3y=0,F1,F2分别是双曲线C的左,右焦点,点P在双曲线C上,且|PF1|=2,则|PF2|等于( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
14. 如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )
如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )
 如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )
如图,一块长宽分别为30M、40M的矩形草地,其中间及四角是半径为10M的圆和扇形花圃,随意向草地浇水,则浇在花圃中的概率为( )| A. | $\frac{π}{12}$ | B. | $1-\frac{π}{6}$ | C. | $\frac{π}{6}$ | D. | $1-\frac{π}{12}$ |
11.设$\overrightarrow a=(1\;,\;2)\;,\;\overrightarrow b=(1\;,\;1)$,$\overrightarrow c=\overrightarrow a+k\overrightarrow b$,若$\overrightarrow b⊥\overrightarrow c$,则实数k=( )
| A. | $-\frac{3}{2}$ | B. | $-\frac{5}{3}$ | C. | $\frac{5}{3}$ | D. | $\frac{3}{2}$ |
15.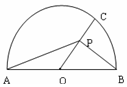 如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )
如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )
 如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )
如图,半圆的直径AB=4,O为圆心,C为半圆上不同A,B的任意一点,若P为半径OC上的动点,则($\overrightarrow{PA}+\overline{PB}$)•$\overline{PC}$的最小值等于( )| A. | 2 | B. | -1 | C. | -2 | D. | 0 |
13.设a=log0.80.9,b=log1.10.9,c=1.10.9,则a,b,c的大小关系是( )
| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
