题目内容
求下列函数的导数.
(1)y=2xsin(2x-5)
(2)f(x)=ln
(3)y=
.
(1)y=2xsin(2x-5)
(2)f(x)=ln
| x2+1 |
(3)y=
| 2x |
| x2+1 |
考点:导数的运算
专题:导数的概念及应用
分析:根据导数公式和运算法则以及复合函数的求导法则计算即可.y′=(2x)′sin(2x-5)+2x[sinx(2x-5)]′iiiii
解答:
解:(1)y′=(2x)′sin(2x-5)+2x[sinx(2x-5)]′
=2sin(2x-5)+2x(2x-5)′cos(2x-5)
=2sin(2x-5)+4xcos(2x-5).
(2)f′(x)=
(
)′=
×
(x2+1)-
(x2+1)′=
.
(3)y′=
=
=2sin(2x-5)+2x(2x-5)′cos(2x-5)
=2sin(2x-5)+4xcos(2x-5).
(2)f′(x)=
| 1 | ||
|
| x2+1 |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
| x |
| x2+1 |
(3)y′=
| 2(x2+1)-2x•2x |
| (x2+1)2 |
| 2-2x2 |
| (x2+1)2 |
点评:本题主要考查了初等函数导数公式以及复合函数的求导法则和导数的运算法则,属于基础题.

练习册系列答案
相关题目
 如图,△ABC的三个内角分别为A,B,C,cosA=
如图,△ABC的三个内角分别为A,B,C,cosA= 如图,点A是单位圆与x轴正半轴的交点,点B(-
如图,点A是单位圆与x轴正半轴的交点,点B(-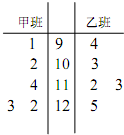 为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图:
为了解甲、乙两个班级某次考试的数学成绩,从甲、乙两个班级中分别随机抽取5名学生的成绩(单位:分)作样本,如图是样本的茎叶图: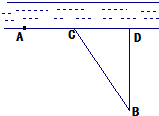 甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,
甲、乙两个工厂,甲厂位于一直线河岸的岸边A处,乙厂与甲厂在河的同侧,乙厂位于离河岸40千米的B处,乙厂到河岸的垂足D与A相距50千米,两厂要在此岸边AD之间合建一个供水站C,从供水站到甲厂和乙厂的水管费用分别为每千米3a元和5a元,若CD=x千米,设总的水管费用为y元,如图所示,