题目内容
已知数列{an}是等比数列，若a1•a5=9，则a3=（ ）
| A、±3 | ||
| B、-3 | ||
| C、3 | ||
D、
|
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：直接由等比数列的性质结合已知条件求得a3的值．
解答：
解：∵数列{an}是等比数列，且a1•a5=9，
由等比数列的性质得：a32=a1•a5=9，
∴a3=±3．
故选：A．
由等比数列的性质得：a32=a1•a5=9，
∴a3=±3．
故选：A．
点评：本题考查了等比数列的性质，是基础的计算题．
练习册系列答案
相关题目
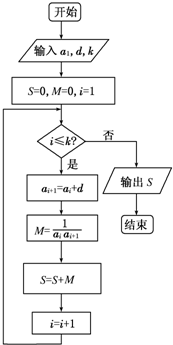已知等差数列{an}的各项均为正数，观察如图所示的程序框图，当k=5，k=10时，分别有S=| 5 |
| 11 |
| 10 |
| 21 |
| A、an=2n+1 |
| B、an=2n+3 |
| C、an=2n-1 |
| D、an=2n-3 |
下列函数中既是偶函数，又在（-1，0）上为减函数的是（ ）
| A、y=cosx | ||
| B、y=-|x-1| | ||
C、y=ln
| ||
| D、y=ex+e-x |
若f（x）为R上的偶函数，g（x）=f（x-1）为R上的奇函数，且g（1）=2，则f（2014）的值为（ ）
| A、1 | B、2 | C、-1 | D、-2 |
在数列{an}中，a1=3，an+1=an+lg（1+
）（n∈N*），则an=（ ）
| 1 |
| n |
| A、lgn | ||||||
B、3+lg（
| ||||||
| C、3+lgn | ||||||
| D、3+3lng |