题目内容
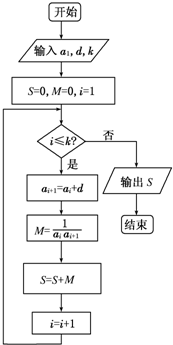 已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=
已知等差数列{an}的各项均为正数,观察如图所示的程序框图,当k=5,k=10时,分别有S=| 5 |
| 11 |
| 10 |
| 21 |
| A、an=2n+1 |
| B、an=2n+3 |
| C、an=2n-1 |
| D、an=2n-3 |
考点:程序框图
专题:算法和程序框图
分析:由程序框图可知其功能为计算输出S=
+
+…+
,由于{an}是等差数列,其公差为d,则有
=
(
-
),k=5时,S=
;k=10时,S=
,从而可求其通项公式.
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| akak+1 |
| 1 |
| akak+1 |
| 1 |
| d |
| 1 |
| ak |
| 1 |
| ak+1 |
| 5 |
| 11 |
| 10 |
| 21 |
解答:
解:由程序框图可知,S=
+
+…+
,
∵{an}是等差数列,其公差为d,则有
=
(
-
),
∴S=
(
-
+
-
+…+
-
)
=
(
-
),
由题意可知,k=5时,S=
;k=10时,S=
,
∴
;解得
或
(舍去),
故an=a1+(n-1)d=2n-1.(n∈N*)
故选:C.
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| akak+1 |
∵{an}是等差数列,其公差为d,则有
| 1 |
| akak+1 |
| 1 |
| d |
| 1 |
| ak |
| 1 |
| ak+1 |
∴S=
| 1 |
| d |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| ak |
| 1 |
| ak+1 |
=
| 1 |
| d |
| 1 |
| a1 |
| 1 |
| ak+1 |
由题意可知,k=5时,S=
| 5 |
| 11 |
| 10 |
| 21 |
∴
|
|
|
故an=a1+(n-1)d=2n-1.(n∈N*)
故选:C.
点评:本题主要考察程序框图和算法以及等差数列通项公式的求法,属于中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
集合A={-1,0,1}的真子集共有( )个.
| A、2个 | B、5个 | C、7个 | D、8个 |
△ABC的内角A、B、C的对边分别为a、b、c.若a、b、c成等比数列且c=2a,则sinB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}是等比数列,若a1•a5=9,则a3=( )
| A、±3 | ||
| B、-3 | ||
| C、3 | ||
D、
|