题目内容
已知b=-a2+3lna,d=c+2,则(a-c)2+(b-d)2的最小值为( )
A、
| ||
| B、2 | ||
C、2
| ||
| D、8 |
考点:导数在最大值、最小值问题中的应用,函数的最值及其几何意义,直线与圆锥曲线的关系
专题:导数的综合应用,圆锥曲线中的最值与范围问题
分析:设b=y,a=x,则y=3lnx-x2,设c=x,d=y,则y=x+2,从而(a-c)2+(b-d)2就是曲线y=3lnx-x2与直线y=x+2之间的最小距离的平方值,由此能求出(a-c)2+(b-d)2的最小值.
解答:
解:∵b=-a2+3lna,设b=y,a=x,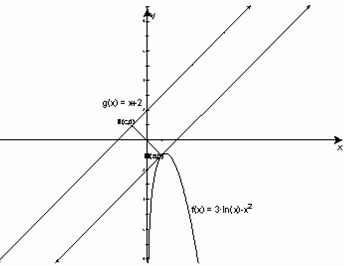
∴y=3lnx-x2
∵d=c+2,设c=x,d=y,∴y=x+2,
∴(a-c)2+(b-d)2
就是曲线y=3lnx-x2与直线y=x+2之间的最小距离的平方值,
对曲线y=3lnx-x2求导:y'(x)=
-2x,
与y=x+2平行的切线斜率k=1=
-2x,
解得:x=1或x=-
(舍)
把x=1代入y=3lnx-x2,得:y=-1,
即切点为(1,-1),
切点到直线y=x+2的距离:
=2
,
∴(a-c)2+(b-d)2的最小值就是8.
故选:D.

∴y=3lnx-x2
∵d=c+2,设c=x,d=y,∴y=x+2,
∴(a-c)2+(b-d)2
就是曲线y=3lnx-x2与直线y=x+2之间的最小距离的平方值,
对曲线y=3lnx-x2求导:y'(x)=
| 3 |
| x |
与y=x+2平行的切线斜率k=1=
| 3 |
| x |
解得:x=1或x=-
| 3 |
| 2 |
把x=1代入y=3lnx-x2,得:y=-1,
即切点为(1,-1),
切点到直线y=x+2的距离:
| |1+1+2| | ||
|
| 2 |
∴(a-c)2+(b-d)2的最小值就是8.
故选:D.
点评:本题考查代数和的最小值的求法,是中档题,解题时要注意等价转化思想的合理运用.

练习册系列答案
相关题目
根据表格内的数据,可以断定方程ex-x-2=0的一个根所在的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.08 |
| x+2 | 1 | 2 | 3 | 4 | 5 |
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |