题目内容
3.设实数x,y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-3≥0}\\{x≤2}\end{array}\right.$,则$\frac{y}{x}$的取值范围是( )| A. | [$\frac{1}{2}$,8] | B. | [$\frac{1}{2}$,3] | C. | [3,8] | D. | [$\frac{1}{2}$,+∞) |
分析 由约束条件作出可行域,数形结合求得 $\frac{y}{x}$的取值范围.
解答 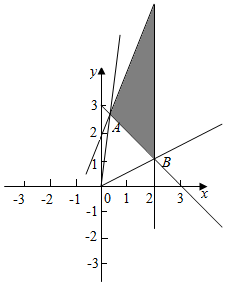 解:由约束条件$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-3≥0}\\{x≤2}\end{array}\right.$,作出可行域如
解:由约束条件$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-3≥0}\\{x≤2}\end{array}\right.$,作出可行域如
由$\left\{\begin{array}{l}{y=2x+2}\\{x+y-3=0}\end{array}\right.$,求得A($\frac{1}{3}$,$\frac{8}{3}$),由$\left\{\begin{array}{l}{x=2}\\{x+y-3=0}\end{array}\right.$,解得B(2,1),利用斜率公式得结合图形可知$\frac{y}{x}$的取值范围是[$\frac{1}{2}$,8].
故选:A.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
16.直线xcosα-y+sinα=0,则该直线倾斜角的取值范围是( )
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | C. | [0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
11.已知直线l:y=kx+b,曲线C:x2+y2-2x=0,则“k+b=0”是“直线l与曲线C有公共点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.设向量$\overrightarrow a$=(1,2),$\overrightarrow b$=(1,1),$\overrightarrow c$=$\overrightarrow a$+k$\overrightarrow b$,若$\overrightarrow b$⊥$\overrightarrow c$,则实数k的值等于( )
| A. | $-\frac{3}{2}$ | B. | $-\frac{5}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{3}$ |
15.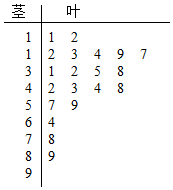 近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:
近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:
(1)完成如下的频率分布表,并在所给的坐标系中画出(0,100)的频率分布直方图;
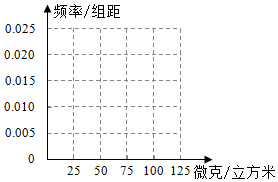 (2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
 近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:
近期雾霾天气多发,对城市环境造成很大影响,某城市环保部门加强了对空气质量的检测,按国家环保部门发布的《环境空气质量标准》的规定:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.抽取某居民区监控点记录的20天PM2.5的24小时平均浓度的监测数据,数集记录为如图茎叶图:(1)完成如下的频率分布表,并在所给的坐标系中画出(0,100)的频率分布直方图;
| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | ||
| 第二组 | (25,50] | ||
| 第三组 | (50,75] | ||
| 第四组 | (75,100] |
 (2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
(2)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
12.过点(4,0)且斜率为-$\frac{\sqrt{3}}{3}$的直线交圆x2+y2-4x=0于A,B两点,则弦长|AB|等于( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
13.从甲、乙、丙、丁四个人中选两名代表,甲被选中的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |