题目内容
12.过点(4,0)且斜率为-$\frac{\sqrt{3}}{3}$的直线交圆x2+y2-4x=0于A,B两点,则弦长|AB|等于( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
分析 写出直线方程,化圆的一般方程为标准方程,求出圆心坐标和半径,求出圆心到直线l的距离,再用勾股定理求出弦AB的一半,再求出玹AB的长.
解答 解:∵直线过点(4,0)且斜率为-$\frac{\sqrt{3}}{3}$,
∴直线AB的方程为y-0=-$\frac{\sqrt{3}}{3}$(x-4),即$\sqrt{3}$x+3y-$4\sqrt{3}$=0.
圆x2+y2-4x=0化为(x-2)2+y2=4,圆心(2,0)到直线AB的距离为d=$\frac{|2\sqrt{3}+3×0-4\sqrt{3}|}{\sqrt{(\sqrt{3})^{2}+{3}^{2}}}=\frac{2\sqrt{3}}{2\sqrt{3}}=1$.
∴AB=$2\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{4-1}=2\sqrt{3}$.
故选:A.
点评 本题考查直线和圆的位置关系、弦长求法,训练了点到直线距离公式的应用,是基础题.

练习册系列答案
相关题目
3.设实数x,y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-3≥0}\\{x≤2}\end{array}\right.$,则$\frac{y}{x}$的取值范围是( )
| A. | [$\frac{1}{2}$,8] | B. | [$\frac{1}{2}$,3] | C. | [3,8] | D. | [$\frac{1}{2}$,+∞) |
20.执行如图的程序框图,若t输入(a,a+1)中的数值,输出的S是单调增加的,则实数a的取值范围是( )
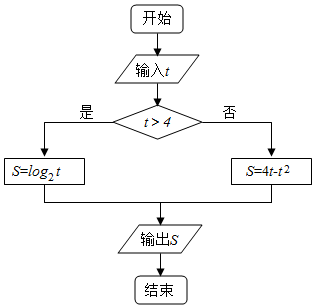

| A. | (-∞,1) | B. | [1,4] | C. | (-∞,1]∪(4,+∞) | D. | (-∞,1]∪[4,+∞) |
7.已知x,y满足$\left\{\begin{array}{l}{x≥2}\\{y≥2}\\{x+y≤8}\end{array}\right.$时,z=x-y的最大值为( )
| A. | 4 | B. | -4 | C. | 0 | D. | 2 |
17.已知函数f(x)=$\left\{\begin{array}{l}{1+{4}^{x},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则f(f($\frac{\sqrt{2}}{4}$))等于( )
| A. | $\frac{9}{8}$ | B. | $\frac{5}{4}$ | C. | $\frac{11}{8}$ | D. | $\frac{7}{4}$ |