题目内容
8．设向量$\overrightarrow a$=（1，2），$\overrightarrow b$=（1，1），$\overrightarrow c$=$\overrightarrow a$+k$\overrightarrow b$，若$\overrightarrow b$⊥$\overrightarrow c$，则实数k的值等于（ ）| A． | $-\frac{3}{2}$ | B． | $-\frac{5}{3}$ | C． | $\frac{3}{2}$ | D． | $\frac{5}{3}$ |
分析 由已知向量的坐标求得向量$\overrightarrow{c}$的坐标，然后由向量垂直的坐标表示列式求得k的值．
解答 解：∵$\overrightarrow a=（{1，2}），\overrightarrow b=（{1，1}），\overrightarrow c=\overrightarrow a+k\overrightarrow b$，
∴$\overrightarrow{c}=（1，2）+k（1，1）=（1+k，2+k）$，
又$\overrightarrow b⊥\overrightarrow c$，∴1×（1+k）+1×（2+k）=0，
即2k+3=0，解得：k=-$\frac{3}{2}$．
故选：A．
点评 本题考查平面向量的数量积运算，考查了数量积的坐标表示，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
2．设Sn是等差数列{an}的前n项和，若$\frac{{S}_{3}}{{S}_{6}}$=$\frac{1}{4}$，则$\frac{{S}_{6}}{{S}_{12}}$=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{8}$ |
16．若指数函数y=（2a-1）x在R上为单调递减函数，则a的取值范围是（ ）
| A． | （0，1） | B． | （$\frac{1}{2}$，+∞） | C． | （$\frac{1}{2}$，+1） | D． | （1，+∞） |
3．设实数x，y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-3≥0}\\{x≤2}\end{array}\right.$，则$\frac{y}{x}$的取值范围是（ ）
| A． | [$\frac{1}{2}$，8] | B． | [$\frac{1}{2}$，3] | C． | [3，8] | D． | [$\frac{1}{2}$，+∞） |
13．
已知函数f（x）和g（x）是两个定义在区间M上的函数，若对任意的x∈M，存在常数x0∈M，使的f（x）≥f（x0），g（x）≥g（x0），且f（x0）=g（x0），则称f（x）与g（x）在区间M上是“相似函数”，若f（x）=2x3-3（a+1）x2+6ax+b与g（x）=x+$\frac{4}{x}$在区间[1，3]上是“相似函数”，则a，b的值分别是（ ）
已知函数f（x）和g（x）是两个定义在区间M上的函数，若对任意的x∈M，存在常数x0∈M，使的f（x）≥f（x0），g（x）≥g（x0），且f（x0）=g（x0），则称f（x）与g（x）在区间M上是“相似函数”，若f（x）=2x3-3（a+1）x2+6ax+b与g（x）=x+$\frac{4}{x}$在区间[1，3]上是“相似函数”，则a，b的值分别是（ ）| A． | a=-2，b=0 | B． | a=-2，b=-2 | C． | a=2，b=0 | D． | a=2，b=-2 |
20．执行如图的程序框图，若t输入（a，a+1）中的数值，输出的S是单调增加的，则实数a的取值范围是（ ）
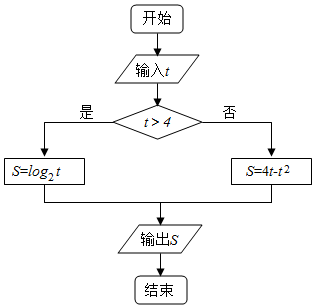
| A． | （-∞，1） | B． | [1，4] | C． | （-∞，1]∪（4，+∞） | D． | （-∞，1]∪[4，+∞） |
17．已知函数f（x）=$\left\{\begin{array}{l}{1+{4}^{x}，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，则f（f（$\frac{\sqrt{2}}{4}$））等于（ ）
| A． | $\frac{9}{8}$ | B． | $\frac{5}{4}$ | C． | $\frac{11}{8}$ | D． | $\frac{7}{4}$ |