题目内容
已知关于x的方程x2+2
x-b+4=0（*），
（Ⅰ）两次抛掷一枚质地均匀的骰子，第一、二次得到的点数分别记为a，b，求使方程（*）有解的概率；
（Ⅱ）在区间[0，6]上分别任意取两个值作为a，b的值，求使方程（*）有解的概率．
| a |
（Ⅰ）两次抛掷一枚质地均匀的骰子，第一、二次得到的点数分别记为a，b，求使方程（*）有解的概率；
（Ⅱ）在区间[0，6]上分别任意取两个值作为a，b的值，求使方程（*）有解的概率．
考点：几何概型,古典概型及其概率计算公式
专题：综合题,概率与统计
分析：（Ⅰ）由方程（*）有解，得△=4a+4b-16≥0⇒a+b≥4．基本事件共6×6=36个，其中a+b≥4基本事件有36-3=33个，由此能求出方程有实根的概率．
（Ⅱ）全部结果所构成的区域为{（a，b）|0≤a≤6，0≤b≤6}，其面积为S=6×6=36，又构成事件A的区域为{（a，b）|0≤a≤6，0≤b≤6，a+b≥4}，求出其面积，由此能求出方程有实根的概率．
（Ⅱ）全部结果所构成的区域为{（a，b）|0≤a≤6，0≤b≤6}，其面积为S=6×6=36，又构成事件A的区域为{（a，b）|0≤a≤6，0≤b≤6，a+b≥4}，求出其面积，由此能求出方程有实根的概率．
解答：
解：方程（*）的判别式△=(2
)2-4×(-b+4)=4a+4b-16
由方程（*）有解，得△=4a+4b-16≥0⇒a+b≥4
（I）两次抛掷一枚质地均匀的骰子全部结果如下：
…（4分）
从而基本事件的总个数为36，其中使△≥0，即a+b≥4的有36-3=33个，
所以方程（*）有解的概率P=
=
…（6分）
（II）如图建立平面直角坐标系：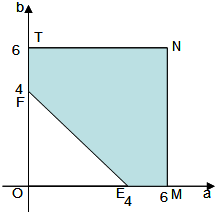
a，b分别用横纵轴来表示，当坐标平面上的点在直线EF的右上方时，a+b≥4，
方程（*）有解，
所以方程（*）有解的概率P=1-
=1-
=
（12分）
| a |
由方程（*）有解，得△=4a+4b-16≥0⇒a+b≥4
（I）两次抛掷一枚质地均匀的骰子全部结果如下：
a b |
1 | 2 | 3 | 4 | 5 | 6 |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
| 5 | （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
| 6 | （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
从而基本事件的总个数为36，其中使△≥0，即a+b≥4的有36-3=33个，
所以方程（*）有解的概率P=
| 33 |
| 36 |
| 11 |
| 12 |
（II）如图建立平面直角坐标系：
a，b分别用横纵轴来表示，当坐标平面上的点在直线EF的右上方时，a+b≥4，方程（*）有解，
所以方程（*）有解的概率P=1-
| S△OEF |
| SOMNT |
| ||
| 36 |
| 7 |
| 9 |
点评：本题考查古典概率、几何概型概率及其运算公式，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
