题目内容
若关于x的不等式a2-4+4x-x2＞0成立时，不等式|x2-4|＜1成立，则正数a的取值范围是 ．
考点：其他不等式的解法
专题：函数的性质及应用,不等式的解法及应用
分析：先求出|x2-4|＜1时x的取值范围，把a2-4+4x-x2＞0变形为a2＞x2-4x+4=（x-2）2；
求出f（x）=（x-2）2在x∈（-
，-
）∪（
，
）时的最大值f（x）max，从而求出a的取值范围．
求出f（x）=（x-2）2在x∈（-
| 5 |
| 3 |
| 3 |
| 5 |
解答：
解：∵|x2-4|＜1，
∴-1＜x2-4＜1，
即3＜x2＜5，
解得-
＜x＜-
，或
＜x＜
；
又∵a2-4+4x-x2＞0，
∴a2＞x2-4x+4=（x-2）2；
设f（x）=（x-2）2，定义域为x∈（-
，-
）∪（
，
），
当x＜2时，f（x）是减函数，x≥2时，f（x）是增函数，
且2-（-
）＞2-
，
∴f（x）max=f（-
），
即a2＞f（-
）；
解得a＞
+2，或a＜-2-
，
又∵a＞0，∴a＞
+2．
∴a的取值范围是a＞
+2．
故答案为：a＞
+2．
∴-1＜x2-4＜1，
即3＜x2＜5，
解得-
| 5 |
| 3 |
| 3 |
| 5 |
又∵a2-4+4x-x2＞0，
∴a2＞x2-4x+4=（x-2）2；
设f（x）=（x-2）2，定义域为x∈（-
| 5 |
| 3 |
| 3 |
| 5 |
当x＜2时，f（x）是减函数，x≥2时，f（x）是增函数，
且2-（-
| 5 |
| 5 |
∴f（x）max=f（-
| 5 |
即a2＞f（-
| 5 |
解得a＞
| 5 |
| 5 |
又∵a＞0，∴a＞
| 5 |
∴a的取值范围是a＞
| 5 |
故答案为：a＞
| 5 |
点评：本题考查了函数性质的应用问题，也考查了不等式的解法与应用问题，解题的关键是转化不等式a2-4+4x-x2＞0，是中档题目．
练习册系列答案
相关题目
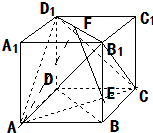如图所示，在正方形ABCD-A1B1C1D1中，E、F分别是BB1、D1B1的中点．求证：EF⊥平面B1AC．已知命题p：2x2-x-1＜0，那么p成立的一个必要不充分条件是（ ）
| A、0＜x＜1 | ||
| B、-1＜x＜1 | ||
C、-
| ||
D、-
|
