题目内容
已知G点为△ABC的重心，且
⊥
，若
+
=
，则实数λ的值为 ．
| AG |
| BG |
| 1 |
| tanA |
| 1 |
| tanB |
| 2λ |
| tanC |
考点：向量在几何中的应用
专题：计算题,解三角形
分析：首先根据三角形的重心性质及直角三角形的斜边的中线等于斜边的一半，得到CD=
AB，再应用余弦定理推出AC2+BC2=5AB2，将
+
=
应用三角恒等变换公式化简得λ=
，然后运用正弦定理和余弦定理，结合前面的结论，即可求出实数λ的值．
| 3 |
| 2 |
| 1 |
| tanA |
| 1 |
| tanB |
| 2λ |
| tanC |
| sin2C |
| 2sinAsinBcosC |
解答：
解：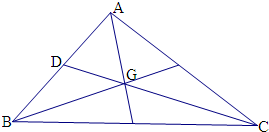
如图，连接CG，延长交AB于D，
由于G为重心，故D为中点，
∵AG⊥BG，∴DG=
AB，
由重心的性质得，CD=3DG，即CD=
AB，
由余弦定理得，AC2=AD2+CD2-2AD•CD•cos∠ADC，
BC2=BD2+CD2-2BD•CD•cos∠BDC，
∵∠ADC+∠BDC=π，AD=BD，
∴AC2+BC2=2AD2+2CD2，
∴AC2+BC2=
AB2+
AB2=5AB2，
又∵
+
=
，
∴
+
=
，
∴λ=
=
=
=
=
=
．
即λ=
．
故答案为：
．
如图，连接CG，延长交AB于D，由于G为重心，故D为中点，
∵AG⊥BG，∴DG=
| 1 |
| 2 |
由重心的性质得，CD=3DG，即CD=
| 3 |
| 2 |
由余弦定理得，AC2=AD2+CD2-2AD•CD•cos∠ADC，
BC2=BD2+CD2-2BD•CD•cos∠BDC，
∵∠ADC+∠BDC=π，AD=BD，
∴AC2+BC2=2AD2+2CD2，
∴AC2+BC2=
| 1 |
| 2 |
| 9 |
| 2 |
又∵
| 1 |
| tanA |
| 1 |
| tanB |
| 2λ |
| tanC |
∴
| cosA |
| sinA |
| cosB |
| sinB |
| 2λcosC |
| sinC |
∴λ=
| (sinAcosB+cosAsinB)sinC |
| 2sinAsinBcosC |
=
| sin2C |
| 2sinAsinBcosC |
=
| AB2 |
| 2BC•AC•cosC |
=
| AB2 |
| BC2+AC2-AB2 |
=
| AB2 |
| 5AB2-AB2 |
=
| 1 |
| 4 |
即λ=
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题主要考查解三角形中的正弦定理与余弦定理及应用，考查三角恒等变换，三角形的重心的性质，考查运算能力，有一定的难度．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
如图中正方体，已知|AG|=|A1G1|，|AH|=|A1H1|，求证：GH∥G1H1，且|GH|=|G1H1|．