题目内容
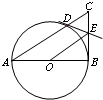以Rt△ABC的直角边AB为直径作圆O，圆O与斜边AC交于D，过D作圆O的切线与BC交于E，若BC=6，AB=8，则OE=考点：圆的切线的性质定理的证明
专题：立体几何
分析：利用条件，可以证明EB=ED=EC，再利用三角形的中位线，即可求得OE的长．
解答：
解：由题意，连接OD，BD，则OD⊥ED，BD⊥AD
∵OB=OD，OE=OE
∴Rt△EBO≌Rt△EDO
∴EB=ED，
∴∠EBD=∠EDB
又∠EBD+∠C=90°，∠EDB+∠EDC=90°
∴∠C=∠EDC，
∴ED=EC
∴EB=EC
∵O是AB的中点，
∴OE=
AC
∵直角边BC=6，AB=8，
∴AC=10，
∴OE=5，
故答案为：5
∵OB=OD，OE=OE ∴Rt△EBO≌Rt△EDO
∴EB=ED，
∴∠EBD=∠EDB
又∠EBD+∠C=90°，∠EDB+∠EDC=90°
∴∠C=∠EDC，
∴ED=EC
∴EB=EC
∵O是AB的中点，
∴OE=
| 1 |
| 2 |
∵直角边BC=6，AB=8，
∴AC=10，
∴OE=5，
故答案为：5
点评：本题考查圆的切线的性质，考查圆的性质，考查三角形中位线的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
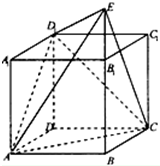如图，直四棱柱ABCD-A1B1C1D1中，底面ABCD为菱形，且∠BAD=60°，A1A=AB，E为BB1延长线上的一点，D1E⊥面D1AC，设AB=2．
如图，在底面边长为a的正方形的四棱锥P-ABCD中，已知PA⊥平面AC，且PA=a，则直线PB与平面PCD所成的角大小为函数y=(
)x2+1(x∈[-1，2])的值域为（ ）
| 1 |
| 2 |
A、[
| ||||
B、(0，
| ||||
C、[
| ||||
D、[
|