题目内容
已知关于x的不等式:|2x-m|≤1的整数解有且仅有一个值为2.
(Ⅰ)求整数m的值;
(Ⅱ)已知a,b,c∈R,若4a4+4b4+4c4=m,求a2+b2+c2的最大值.
(Ⅰ)求整数m的值;
(Ⅱ)已知a,b,c∈R,若4a4+4b4+4c4=m,求a2+b2+c2的最大值.
考点:二维形式的柯西不等式,绝对值不等式的解法
专题:不等式的解法及应用
分析:(I)由条件可得
≤2≤
,求得3≤m≤5.根据不等式仅有一个整数解2,可得整数m的值.
(2)根据a4+b4+c4=1,利用柯西不等式求得(a2+b2+c2)2≤3,从而求得a2+b2+c2的最大值.
| m-1 |
| 2 |
| m+1 |
| 2 |
(2)根据a4+b4+c4=1,利用柯西不等式求得(a2+b2+c2)2≤3,从而求得a2+b2+c2的最大值.
解答:
解:(I)由|2x-m|≤1,得
≤x≤
.∵不等式的整数解为2,∴
≤2≤
⇒3≤m≤5.
又不等式仅有一个整数解2,∴m=4.
(2)由(1)知,m=4,故a4+b4+c4=1,
由柯西不等式可知;(a2+b2+c2)2≤(12+12+12)[(a2)2+(b2)2+(c2)2]
所以(a2+b2+c2)2≤3,即a2+b2+c2≤
,
当且仅当a2=b2=c2=
时取等号,最大值为
.
| m-1 |
| 2 |
| m+1 |
| 2 |
| m-1 |
| 2 |
| m+1 |
| 2 |
又不等式仅有一个整数解2,∴m=4.
(2)由(1)知,m=4,故a4+b4+c4=1,
由柯西不等式可知;(a2+b2+c2)2≤(12+12+12)[(a2)2+(b2)2+(c2)2]
所以(a2+b2+c2)2≤3,即a2+b2+c2≤
| 3 |
当且仅当a2=b2=c2=
| ||
| 3 |
| 3 |
点评:本题主要考查绝对值不等式的解法,二维形式的柯西不等式的应用,属于基础题.

练习册系列答案
相关题目
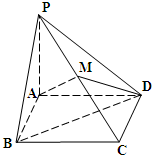 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,点M是棱PC的中点,AM⊥平面PBD.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥底面ABCD,点M是棱PC的中点,AM⊥平面PBD.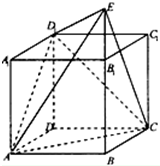 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且∠BAD=60°,A1A=AB,E为BB1延长线上的一点,D1E⊥面D1AC,设AB=2.