题目内容
已知双曲线C与双曲线x2-
=1有共同的渐近线,且双曲线C过点M(2,2),则过点A(1,1)能否作直线l,使l与双曲线C交于Q1、Q2两点,且A是线段Q1Q2的中点,这样的直线l如果存在,求出它的方程;如果不存在,说明理由.
| y2 |
| 2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出双曲线方程,假设直线l存在.由已知条件利用点差法求出直线l的方程为2x-y-1=0,y=2x-1代入双曲线方程,得2x2-4x+5=0,由△<0,推导出直线l不存在.
解答:
解:设双曲线方程为x2-
=λ
代入点M(2,2),得λ=2,
∴双曲线C的方程为
-
=1
设点Q1(x1,y1),Q2(x2,y2),则2x12-y12=4,2x22-y22=4
由点差法作差,利用A是线段Q1Q2的中点,代入得k=2
∴直线l的方程为y-1=2(x-1)即y=2x-1
y=2x-1代入双曲线方程,得2x2-4x+5=0
∵△=16-4×2×5=-24<0,
∴直线l与双曲线C无交点,故直线l不存在.
| y2 |
| 2 |
代入点M(2,2),得λ=2,
∴双曲线C的方程为
| x2 |
| 2 |
| y2 |
| 4 |
设点Q1(x1,y1),Q2(x2,y2),则2x12-y12=4,2x22-y22=4
由点差法作差,利用A是线段Q1Q2的中点,代入得k=2
∴直线l的方程为y-1=2(x-1)即y=2x-1
y=2x-1代入双曲线方程,得2x2-4x+5=0
∵△=16-4×2×5=-24<0,
∴直线l与双曲线C无交点,故直线l不存在.
点评:本题考查双曲线方程、直线方程的求法,是中档题,解题时要认真审题,注意点差法和根的判别式的合理运用.

练习册系列答案
相关题目
下面几个推理过程是演绎推理的是( )
| A、某同学第一次数学考试65分,第二次考试68分,由此预测其第三次考试71分 | ||
| B、根据圆的面积为S=πr2,推测球的体积为V=πr3 | ||
C、在数列{an}中,根据a1=1,an+1=
| ||
| D、因为平行四边形的对角线互相平分,而菱形是平行四边形,所以菱形的对角线互相平分 |
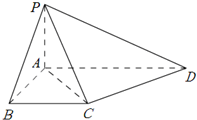 如图,在四棱锥P-ABCD,PA⊥平面ABCD,PA=AB=BC=
如图,在四棱锥P-ABCD,PA⊥平面ABCD,PA=AB=BC= 空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定.空气质量指数越高,代表空气污染越严重:
空气质量已成为城市居住环境的一项重要指标,空气质量的好坏由空气质量指数确定.空气质量指数越高,代表空气污染越严重: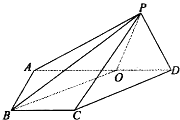 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.