题目内容
已知函数f(x)=
(x∈R)是奇函数.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的值域.
| x+a |
| 2x2+1 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的值域.
考点:函数奇偶性的性质,函数的值域
专题:计算题,函数的性质及应用
分析:(Ⅰ)由于f(x)是奇函数,则f(-x)=-f(x),计算化简即可得到a=0,进而得到解析式;
(Ⅱ)将函数整理成二次方程,先讨论二次项系数为0,再考虑不为0,再由判别式大于0,解得即可得到值域.
(Ⅱ)将函数整理成二次方程,先讨论二次项系数为0,再考虑不为0,再由判别式大于0,解得即可得到值域.
解答:
解:(Ⅰ)∵f(x)是奇函数,
∴f(-x)=-f(x),
又f(-x)=
=-
⇒-x+a=-x-a⇒a=0,
∴f(x)=
;
(Ⅱ)y=
⇒2yx2-x+y=0,
当y=0时,x=0∴y=0成立,
当y≠0时,△=1-4×2y×y≥0⇒-
≤y≤
且y≠0.
综上值域为[-
,
].
∴f(-x)=-f(x),
又f(-x)=
| -x+a |
| 2x2+1 |
| x+a |
| 2x2+1 |
∴f(x)=
| x |
| 2x2+1 |
(Ⅱ)y=
| x |
| 2x2+1 |
当y=0时,x=0∴y=0成立,
当y≠0时,△=1-4×2y×y≥0⇒-
| ||
| 4 |
| ||
| 4 |
综上值域为[-
| ||
| 4 |
| ||
| 4 |
点评:本题考查函数的性质和运用,考查函数的奇偶性和运用,以及函数的值域的求法:判别式法,考查运算能力,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
已知关于x的方程2sin(x+
)-a=0在区间[0,2π]上有两个不同的实根,则实数a的数值范围是( )
| π |
| 3 |
| A、(-2,2) | ||||
| B、[-2,2] | ||||
C、[-2,
| ||||
D、(-2,
|
设[x]表示不超过x的最大整数(如[2]=2,[
]=1).对于给定的n∈N*,定义Cnx=
,x∈[1,+∞),则当x∈[
,3)时,函数f(x)=C8x的值域为( )
| 3 |
| 2 |
| n(n-1)…(n-[x]+1) |
| x(x-1)…(x-[x]+1) |
| 5 |
| 4 |
A、(4,
| ||||
B、(4,
| ||||
C、[4,
| ||||
D、[
|
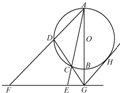 如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.
如图,AB是圆O的直径,G是AB延长线上的一点,GCD是圆O的割线,过点G作AG的垂线,交直线AC于点E,交直线 AD于点F,过点G作圆O的切线,切点为H.