题目内容
4.如图,菱形ABCD的边长为12,∠BAD=60°,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=6$\sqrt{2}$.
(1)求证:OD⊥平面ABC;
(2)求三棱锥M-ABD的体积.
分析 (1)推导出OD⊥AC,DO⊥OM,由此能证明OD⊥面ABC.
(2)由VM-ABD=VD-ABM,能求出三棱锥M-ABD的体积.
解答 满分(12分).
证明:(1)∵ABCD是菱形,AD=DC,OD⊥AC,…(1分)
△ADC中,AD=DC=12,∠ADC=120°,∴OD=6,
又M是BC的中点,∴$OM=\frac{1}{2}AB=6,MD=6\sqrt{2}$,
∵OD2+OM2=MD2,∴DO⊥OM…(4分)
∵OM,AC?面ABC,OM∩AC=O,∴OD⊥面ABC. …(6分)
解:(2)△ABM中,AB=12,BM=6,∠ABM=120°,
∴${S}_{△ABM}=\frac{1}{2}•AB•BM•sin∠ABM$=$\frac{1}{2}•12•6•\frac{\sqrt{3}}{2}$=18$\sqrt{3}$,…(8分)
由(1)得OD⊥面ABC,
∴VM-ABD=VD-ABM=$\frac{1}{3}•OD•{S}_{△ABM}$
=$\frac{1}{3}×6×18\sqrt{3}=36\sqrt{3}$.…(12分)
点评 本题主要考查直线与直线、直线与平面、平面与平面的位置关系及体积计算等基础知识;考查学生的空间想象能力、推理论证能力及运算求解能力;考查了化归与转化及数形结合的数学思想.

练习册系列答案
相关题目
15.某民调机构为了了解民众是否支持英国脱离欧盟,随机抽调了100名民众,他们的年龄的频数及支持英国脱离欧盟的人数分布如下表:
(Ⅰ)由以上统计数据填下面列联表,并判断是否有99%的把握认为以50岁胃分界点对是否支持脱离欧盟的态度有差异;
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
(Ⅱ)若采用分层抽样的方式从18-64岁且支持英国脱离欧盟的民众中选出7人,再从这7人中随机选出2人,求这2人至少有1人年龄在18-24岁的概率.
| 年龄段 | 18-24岁 | 25-49岁 | 50-64岁 | 65岁及以上 |
| 频数 | 35 | 20 | 25 | 20 |
| 支持脱欧的人数 | 10 | 10 | 15 | 15 |
| 年龄低于50岁的人数 | 年龄不低于50岁的人数 | 合计 | |
| 支持“脱欧”人数 | |||
| 不支持“脱欧”人数 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
12.如图所示的程序框图中,输出的B是( )
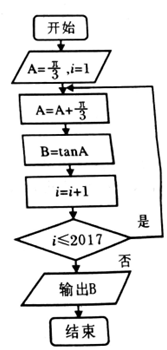

| A. | $\sqrt{3}$ | B. | 0 | C. | -$\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
 如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).
如图,已知平行四边形ABCD的三个顶点的坐标为A(-1,4),B(-2,-1),C(2,3).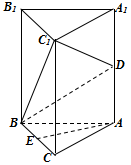 如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.
如图,三棱柱ABC-A1B1C1中,D是AA1的中点,E为BC的中点.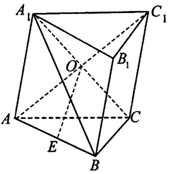 如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1