题目内容
15.下列函数既是奇函数又在定义域上单调递增的是( )| A. | $f(x)=\frac{{{x^2}-2x}}{x-2}$ | B. | f(x)=x-$\frac{1}{x}$ | C. | f(x)=2x-2-x | D. | f(x)=x|sinx| |
分析 根据函数单调性和奇偶性的定义判断即可.
解答 解:对于选项A:f(x)=x,(x≠2),不是奇函数;
选项B:f(x)为奇函数,分别在(-∞,0)和(0,+∞)上单调递增;
选项D:f(x)为奇函数,因为f(0)=f(π),所以在R上不是单调递增;
故选:C.
点评 本题考查了函数的单调性和奇偶性问题,是一道基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
12.如图所示的程序框图中,输出的B是( )
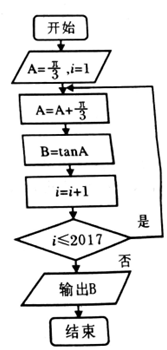

| A. | $\sqrt{3}$ | B. | 0 | C. | -$\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
10.已知某企业的近3年的前7个月的月利润(单位:百万元)如下面的折线图所示:
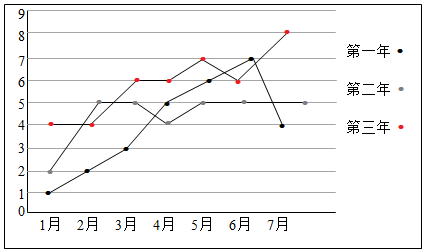
(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
相关公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.

(1)试问这3年的前7个月中哪个月的月平均利润较高?
(2)通过计算判断这3年的前7个月的总利润的发展趋势;
(3)试以第3年的前4个月的数据(如下表),用线性回归的拟合模式估测第3年8月份的利润.
| 月份x | 1 | 2 | 3 | 4 |
| 利润y(单位:百万元) | 4 | 4 | 6 | 6 |
4.设集合M={x|x2≥x},N={x|log${\;}_{\frac{1}{2}}$(x+1)>0},则有( )
| A. | N⊆M | B. | M⊆∁RN | C. | M∩N=∅ | D. | M∪N=R |
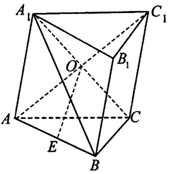 如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
如图,在斜三梭柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1