题目内容
设圆O1和圆O2是两个定圆，动圆P与这两个定圆都相切，则圆P的圆心轨迹可能是
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：先确定圆P的圆心轨迹是焦点为O1、O2，且离心率分别是
和
的圆锥曲线，再分类说明对应的轨迹情况即可．
| 2c |
| r1+r2 |
| 2c |
| |r1-r2| |
解答：
解：设圆O1和圆O2的半径分别是r1、r2，|O1O2|=2c，则
一般地，圆P的圆心轨迹是焦点为O1、O2，且离心率分别是
和
的圆锥曲线．
当r1=r2时，O1O2的中垂线是轨迹的一部份，当c=0时，轨迹是两个同心圆；
当r1=r2且r1+r2＜2c时，圆P的圆心轨迹为一条双曲线和一条直线；
当0＜2c＜|r1-r2|时，圆P的圆心轨迹为两个椭圆；
当r1≠r2且r1+r2＜2c时，圆P的圆心轨迹为两条双曲线．
故答案为：①②④．
一般地，圆P的圆心轨迹是焦点为O1、O2，且离心率分别是
| 2c |
| r1+r2 |
| 2c |
| |r1-r2| |
当r1=r2时，O1O2的中垂线是轨迹的一部份，当c=0时，轨迹是两个同心圆；
当r1=r2且r1+r2＜2c时，圆P的圆心轨迹为一条双曲线和一条直线；
当0＜2c＜|r1-r2|时，圆P的圆心轨迹为两个椭圆；
当r1≠r2且r1+r2＜2c时，圆P的圆心轨迹为两条双曲线．
故答案为：①②④．
点评：本题考查圆与圆的位置关系，考查轨迹问题，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
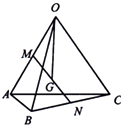已知空间四边形OABC，M，N分别是OA，BC的中点，点G是线段MN的中点，设| OG |
| OA |
| OB |
| OC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
y=Asin（ωx+φ）的曲线最高点为（2，
），离它最近的一个最低点是（10，-
），则它的解析式为（ ）
| 2 |
| 2 |
A、f（x）=
| ||||||
B、f（x）=
| ||||||
C、f(x)=
| ||||||
D、f(x)=-
|