题目内容
y=Asin(ωx+φ)的曲线最高点为(2,
),离它最近的一个最低点是(10,-
),则它的解析式为( )
| 2 |
| 2 |
A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
D、f(x)=-
|
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式.
解答:
解:由题意可得A=
,
T=10-2=8=
,求得ω=
.
再根据五点法作图可得
×2+φ=
,求得φ=
,
∴f(x)=
sin(
x+
),
故选:B.
| 2 |
| 1 |
| 2 |
| π |
| ω |
| π |
| 8 |
再根据五点法作图可得
| π |
| 8 |
| π |
| 2 |
| π |
| 4 |
∴f(x)=
| 2 |
| π |
| 8 |
| π |
| 4 |
故选:B.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,属于基础题.

练习册系列答案
相关题目
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )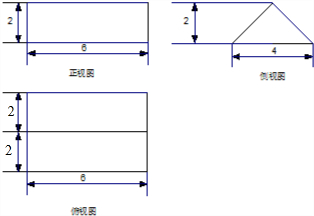

| A、12cm3 | ||
| B、24cm3 | ||
C、
| ||
| D、40cm3 |
已知函数f(x)=(2k-1)x+2在R上是减函数,则实数k的取值范围为( )
A、k<-
| ||
B、k>-
| ||
C、k<
| ||
D、k>
|
已知圆M过定点(2,0)且圆心M在抛物线y2=4x上运动,若y轴截圆M所得的弦长为AB,则弦长|AB|等于( )
| A、4 | B、3 |
| C、2 | D、与点M位置有关的值 |
