题目内容
17.数列{an}为正项等比数列,a1=2,$\frac{3}{8}$a4是a2和a3的等差中项,Sn为数列{bn}前n项和,2b2=b1+b3,$\sqrt{{S}_{n}}$是公差为1的等差数列.(1)求数列{nan}的前n项和Tn;
(2)求数列{bn}通项公式;
(3)是否存在n∈N*,使Sn=an成立?若存在,求出所有n的值,若不存在,说明理由.
分析 (1)数列{an}为正项等比数列,设公比为q,运用等差中项的概念和等比数列的通项公式,解方程可得公比q,再由数列的求和方法:错位相减法,结合等比数列的求和公式,计算即可得到所求和;
(2)运用等差数列的通项公式和特值法,解方程可得首项b1=1,可得Sn=n2,再由数列的递推关系,可得数列{bn}通项公式;
(3)由Sn=an,即n2=2n,n∈N*.可设f(n)=n2-2n,显然f(2)=f(4)=0,运用二项式定理,可得n>4时,f(n)<0,即可得到n的所有值.
解答 解:(1)数列{an}为正项等比数列,设公比为q,
由$\frac{3}{8}$a4是a2和a3的等差中项,可得$\frac{3}{4}$a4=a2+a3,
即有$\frac{3}{4}$a1q3=a1q+a1q2,
化为3q2-4q-4=0,
解得q=2(-$\frac{2}{3}$舍去),
即有an=a1qn-1=2n,
前n项和Tn=1•2+2•22+…+n•2n,
2Tn=1•22+2•23+…+n•2n+1,
相减可得-Tn=2+22+…+2n-n•2n+1=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1,
化简可得Tn=2+(n-1)•2n+1;
(2)$\sqrt{{S}_{n}}$是公差为1的等差数列,
可得$\sqrt{{S}_{n}}$=$\sqrt{{S}_{1}}$+n-1,
即有$\sqrt{{S}_{2}}$=$\sqrt{{b}_{1}}$+1,即b1+b2=b1+1+2$\sqrt{{b}_{1}}$,①
$\sqrt{{S}_{3}}$=$\sqrt{{b}_{1}}$+2,即b1+b2+b3=b1+4+4$\sqrt{{b}_{1}}$,
由2b2=b1+b3,即有3b2=b1+4+4$\sqrt{{b}_{1}}$,②
由①②可得b1+1-2$\sqrt{{b}_{1}}$=0,解得b1=1,
则$\sqrt{{S}_{n}}$=$\sqrt{{S}_{1}}$+n-1=n,可得Sn=n2,
b1=S1=1;n≥2时,bn=Sn-Sn-1=n2-(n-1)2=2n-1,
综上可得数列{bn}通项公式为bn=2n-1,n∈N*;
(3)由Sn=an,即n2=2n,n∈N*.
可设f(n)=n2-2n,显然f(2)=4-4=0;
f(4)=16-16=0,
当n≥5时,f(n)=n2-(1+1)n=n2-(1+n+$\frac{n(n-1)}{2}$+…+$\frac{n(n-1)}{2}$+n+1)<0,
综上可得,存在n∈N*,使Sn=an成立,且n=2和4.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查存在性问题的解法,注意运用构造法,考查数列的求和方法:错位相减法,考查转化思想和运算能力,属于中档题.

 新课标同步训练系列答案
新课标同步训练系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
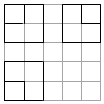 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
| A. | $\frac{{3-4\sqrt{3}}}{10}$ | B. | $\frac{{3+4\sqrt{3}}}{10}$ | C. | $\frac{{-3-4\sqrt{3}}}{10}$ | D. | $\frac{{-3+4\sqrt{3}}}{10}$ |