题目内容
(2013•浙江)如图,点P(0,﹣1)是椭圆C1: +
+ =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.

 +
+ =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.(1)求椭圆C1的方程;
(2)求△ABD面积的最大值时直线l1的方程.

(1) (2)
(2)
 (2)
(2)
(1)由题意可得b=1,2a=4,即a=2.
∴椭圆C1的方程为 ;
;
(2)设A(x1,y1),B(x2,y2),D(x0,y0).
由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx﹣1.
又圆 的圆心O(0,0)到直线l1的距离d=
的圆心O(0,0)到直线l1的距离d= .
.
∴|AB|= =
= .
.
又l2⊥l1,故直线l2的方程为x+ky+k=0,联立 ,消去y得到(4+k2)x2+8kx=0,解得
,消去y得到(4+k2)x2+8kx=0,解得 ,
,
∴ .
.
∴三角形ABD的面积 .
.
∴
 =
= ,当且仅当
,当且仅当 时取等号,
时取等号,
故所求直线l1的方程为 .
.
∴椭圆C1的方程为
 ;
;(2)设A(x1,y1),B(x2,y2),D(x0,y0).
由题意可知:直线l1的斜率存在,设为k,则直线l1的方程为y=kx﹣1.
又圆
 的圆心O(0,0)到直线l1的距离d=
的圆心O(0,0)到直线l1的距离d= .
.∴|AB|=
 =
= .
.又l2⊥l1,故直线l2的方程为x+ky+k=0,联立
 ,消去y得到(4+k2)x2+8kx=0,解得
,消去y得到(4+k2)x2+8kx=0,解得 ,
,∴
 .
.∴三角形ABD的面积
 .
.∴

 =
= ,当且仅当
,当且仅当 时取等号,
时取等号,故所求直线l1的方程为
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .称圆心在原点O,半径为
.称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
. ,使得
,使得 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断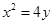 的准线与椭圆
的准线与椭圆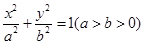 相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )
相切,且该切点与椭圆的两焦点构成的三角形面积为2,则椭圆的离心率是( )



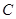 的中心在原点,焦点在
的中心在原点,焦点在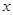 轴上,离心率为
轴上,离心率为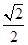 ,它的一个焦点恰好与抛物线
,它的一个焦点恰好与抛物线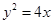 的焦点重合.
的焦点重合. ,过点
,过点 ,若直线
,若直线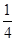 ,直线
,直线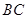 是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由.
是否一定经过一定点?若经过,求出该定点坐标;若不经过,请说明理由. ,离心率等于
,离心率等于 ,则椭圆的方程是( )
,则椭圆的方程是( ) 



 (a>b>0)的左、右焦点,若在直线x=
(a>b>0)的左、右焦点,若在直线x= 上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )



 上的动点,点D是P在
上的动点,点D是P在 轴上投影,M为PD上一点,且
轴上投影,M为PD上一点,且 .
.
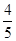 的直线被C所截线段的长度.
的直线被C所截线段的长度.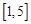 和
和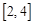 上分别取一个数,记为
上分别取一个数,记为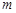 和
和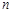 ,则方程
,则方程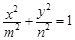 ,表示焦点在y轴上的椭圆的概率是 .
,表示焦点在y轴上的椭圆的概率是 . 的左、右焦点分别为
的左、右焦点分别为 ,点M在该椭圆上,且
,点M在该椭圆上,且 ,则点M到y轴的距离为( )
,则点M到y轴的距离为( )


