题目内容
设F1、F2分别是椭圆 (a>b>0)的左、右焦点,若在直线x=
(a>b>0)的左、右焦点,若在直线x= 上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
 (a>b>0)的左、右焦点,若在直线x=
(a>b>0)的左、右焦点,若在直线x= 上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )A. | B. | C. | D. |
D
设P ,F1P的中点Q的坐标为
,F1P的中点Q的坐标为 ,则kF1P=
,则kF1P= ,kQF2=
,kQF2= .
.
由kF1P·kQF2=-1,
得y2= .
.
因为y2≥0,但注意b2+2c2≠0,
所以2c2-b2>0,即3c2-a2>0.
即e2> .故
.故 <e<1.
<e<1.
当b2-2c2=0时,y=0,此时kQF2不存在,此时F2为中点, -c=2c,得e=
-c=2c,得e= .综上得,
.综上得, ≤e<1.
≤e<1.
 ,F1P的中点Q的坐标为
,F1P的中点Q的坐标为 ,则kF1P=
,则kF1P= ,kQF2=
,kQF2= .
.由kF1P·kQF2=-1,
得y2=
 .
.因为y2≥0,但注意b2+2c2≠0,
所以2c2-b2>0,即3c2-a2>0.
即e2>
 .故
.故 <e<1.
<e<1.当b2-2c2=0时,y=0,此时kQF2不存在,此时F2为中点,
 -c=2c,得e=
-c=2c,得e= .综上得,
.综上得, ≤e<1.
≤e<1.
练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
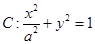 经过点
经过点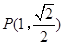 .
.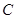 的方程及其离心率;
的方程及其离心率;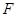 的直线(不经过点
的直线(不经过点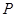 )与椭圆交于
)与椭圆交于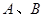 两点,当
两点,当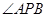 的平分线为
的平分线为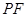 时,求直线
时,求直线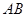 的斜率
的斜率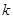 .
.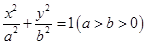 ,
,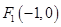 、
、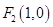 是椭圆的左右焦点,且椭圆经过点
是椭圆的左右焦点,且椭圆经过点 .
.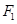 且倾斜角等于
且倾斜角等于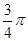 的直线
的直线 ,交椭圆于
,交椭圆于 、
、 两点,求
两点,求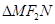 的面积.
的面积.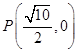 作倾斜角为
作倾斜角为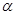 的直线
的直线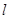 与曲线C
与曲线C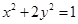 交于不同的两点
交于不同的两点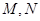 ,求
,求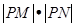 的取值范围.
的取值范围.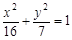 的左右焦点为
的左右焦点为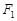 、
、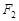 ,一直线过
,一直线过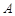 、
、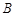 两点,则
两点,则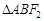 的周长为 ( )
的周长为 ( )  +
+ =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径,l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A、B两点,l2交椭圆C1于另一点D.
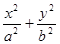 =1(a>b>0)的左、右焦点分别为为
=1(a>b>0)的左、右焦点分别为为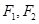 ,
,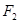 恰是抛物线C2:
恰是抛物线C2: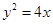 的焦点,点M为C1与C2在第一象限的交点,且|MF2|=
的焦点,点M为C1与C2在第一象限的交点,且|MF2|=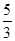 .
.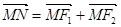 ,直线l∥MN,且与C1交于A,B两点,若
,直线l∥MN,且与C1交于A,B两点,若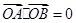 ,求直线l的方程.
,求直线l的方程.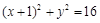 ,点
,点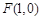 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.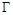 的方程;
的方程;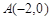 ,
,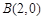 ,点G是轨迹
,点G是轨迹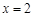 相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.
相交于点D,试判断以线段BD为直径的圆与直线GF的位置关系,并证明你的结论.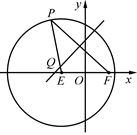
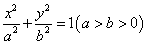 的离心率
的离心率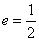 ,右焦点
,右焦点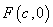 ,方程
,方程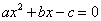 的两个根分别为
的两个根分别为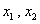 ,则点
,则点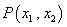 在( )
在( )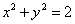 上
上