题目内容
将一枚正方体骰子先后掷两次,所得点数分别为m,n,函数f(x)=
x3+
mx2+nx+3(x∈R).
(1)若第一次得到的点数m=4,求函数f(x)=
x3+
mx2+nx+3与函数g(x)=3的图象有三个交点的概率;
(2)求函数h(x)=f(x)-2nx在(
,+∞)上是增函数的概率.
| 1 |
| 3 |
| 1 |
| 2 |
(1)若第一次得到的点数m=4,求函数f(x)=
| 1 |
| 3 |
| 1 |
| 2 |
(2)求函数h(x)=f(x)-2nx在(
| 1 |
| 2 |
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)根据函数f(x)与g(x)有三个交点得到,得到x(x2+6x+3n)=0有三个不同的解,即x2+6x+3n=0有两个不同的解,根据判别式求出n的值,根据概率公式计算即可.
(2)先求导,得到h′(x)=x2+mx-n>0,在(
,+∞)上恒成立,继而求出m,n的关系,利用数形结合的思想,求出满足条件的基本事件的个数,根据概率公式计算即可.
(2)先求导,得到h′(x)=x2+mx-n>0,在(
| 1 |
| 2 |
解答:
 解:(1)当m=4时,f(x)=
解:(1)当m=4时,f(x)=
x3+2x2+nx+3,
∵f(x)与g(x)=3的图象有三个交点,
∴
x3+2x2+nx+3=3有三个不同的解,
即x(x2+6x+3n)=0有三个不同的解,
∴x2+6x+3n=0有两个不同的解,
∴△=36-12n>0,解得n<3,
∴n=1,2
∵第二次点数的基本事件有6个,
∴函数f(x)=
x3+
mx2+nx+3与函数g(x)=3的图象有三个交点的概率P=
=
;
(2)∵h(x)=f(x)-2nx=
x3+
mx2+nx+3-2nx=
x3+
mx2-nx+3,在(
,+∞)上是增函数,
∴h′(x)=x2+mx-n>0,在(
,+∞)上恒成立,
∴
∴n<
m+
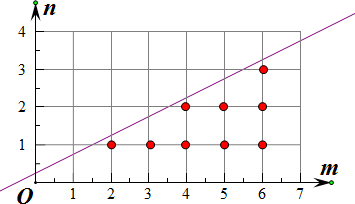
画出函数n=
m+
的图象,如图所示,
则满足条件的点有9个,
而试验发生包含的所有事件数是6×6=36,
∴函数h(x)=f(x)-2nx在(
,+∞)上是增函数的概率P=
=
 解:(1)当m=4时,f(x)=
解:(1)当m=4时,f(x)=| 1 |
| 3 |
∵f(x)与g(x)=3的图象有三个交点,
∴
| 1 |
| 3 |
即x(x2+6x+3n)=0有三个不同的解,
∴x2+6x+3n=0有两个不同的解,
∴△=36-12n>0,解得n<3,
∴n=1,2
∵第二次点数的基本事件有6个,
∴函数f(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 6 |
| 1 |
| 3 |
(2)∵h(x)=f(x)-2nx=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
∴h′(x)=x2+mx-n>0,在(
| 1 |
| 2 |
∴
|
∴n<
| 1 |
| 2 |
| 1 |
| 4 |
画出函数n=
| 1 |
| 2 |
| 1 |
| 4 |
则满足条件的点有9个,
而试验发生包含的所有事件数是6×6=36,
∴函数h(x)=f(x)-2nx在(
| 1 |
| 2 |
| 9 |
| 36 |
| 1 |
| 4 |
点评:本题考查古典概型的概率问题以及函数的解得的个数以及恒成立的问题,培养了学生的转化能力和运算能力,属于中档题.

练习册系列答案
相关题目
已知椭圆的方程为x2+
=1(0<a<1),椭圆上离顶点A(0,a)的最远点为(0,-a),则实数a的取值范围是( )
| y2 |
| a2 |
| A、0<a<1 | ||||
B、
| ||||
C、
| ||||
D、0<a<
|
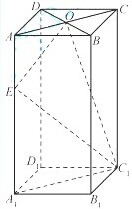 如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.
如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,E为棱AA1上任意一点,F是CD的中点.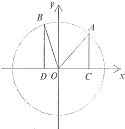 如图,在平面直角坐标系xOY中,点A(x1,y1)在单位圆O上.∠xOA=α且α∈(
如图,在平面直角坐标系xOY中,点A(x1,y1)在单位圆O上.∠xOA=α且α∈( 已知函数f(x)=
已知函数f(x)=