题目内容
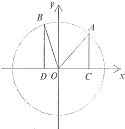 如图,在平面直角坐标系xOY中,点A(x1,y1)在单位圆O上.∠xOA=α且α∈(
如图,在平面直角坐标系xOY中,点A(x1,y1)在单位圆O上.∠xOA=α且α∈(| π |
| 6 |
| π |
| 2 |
(1)若cos(α+
| π |
| 3 |
2
| ||
| 3 |
(2)如图表示,B(x2,y2)也是单位圆O上的点,且∠AOB=
| π |
| 3 |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:(1)由三角函数的定义有y1=sinα,由已知可得sin(α+
)=
,从而由y1=sinα=sin[(α+
)-
]利用两角差的正弦公式即可代入求值.
(2)由y1=sinα,利用二倍角公式可求得S1,由定义得x2,y2,又由α∈(
,
),得α+
∈(
,
),于是可求S2,从而由三角函数中的恒等变换应用可求f(α)=S1+S2=
sin(2α-
),由α∈(
,
),可得2α-
∈(
,
),利用正弦函数的图象和性质即可求得函数f(α)的最大值.
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
| π |
| 3 |
(2)由y1=sinα,利用二倍角公式可求得S1,由定义得x2,y2,又由α∈(
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| ||
| 4 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
解答:
解:(1)由三角函数的定义有y1=sinα,…2分
∵cos(α+
)=-
,且α∈(
,
).
∴sin(α+
)=
,…4分
∴y1=sinα=sin[(α+
)-
]
=sin(α+
)cos
-cos(α+
)sin
=
×
+
×
=
…6分
(2)由y1=sinα,得S1=
x1y1=
cosαsinα=
sin2α,…7分
由定义得x2=cos(α+
),y2=sin(α+
),
又由α∈(
,
),得α+
∈(
,
),
于是,S2=-
x2y2=-
cos(α+
)sin(α+
)=-
sin(2α+
)…9分
∴f(α)=S1+S2=
sin2α-
sin(2α+
)=
sin2α-
(sin2αcos
+cos2αsin
)
=
sin2α-
cos2α=
(
sin2α-
cos2α)=
sin(2α-
),…11分
由α∈(
,
),可得2α-
∈(
,
),
于是当2α-
=
,即α=
时,f(α)max=
…13分
∵cos(α+
| π |
| 3 |
2
| ||
| 3 |
| π |
| 6 |
| π |
| 2 |
∴sin(α+
| π |
| 3 |
| 1 |
| 3 |
∴y1=sinα=sin[(α+
| π |
| 3 |
| π |
| 3 |
=sin(α+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=
| 1 |
| 2 |
| 1 |
| 3 |
2
| ||
| 3 |
| ||
| 2 |
1+2
| ||
| 6 |
(2)由y1=sinα,得S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
由定义得x2=cos(α+
| π |
| 3 |
| π |
| 3 |
又由α∈(
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
于是,S2=-
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 4 |
| 2π |
| 3 |
∴f(α)=S1+S2=
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2π |
| 3 |
| 2π |
| 3 |
=
| 3 |
| 8 |
| ||
| 8 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| π |
| 6 |
由α∈(
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
于是当2α-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| ||
| 4 |
点评:本题主要考查了三角函数中的恒等变换应用,考查了正弦函数的图象和性质,考查了转化思想,属于中档题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
在△ABC中,D为BC上一点,BD=
DC,∠ADB=120°,AD=2,若△ADC的面积为3-
,则∠ABC=( )
| 1 |
| 2 |
| 3 |
| A、30° | B、60° |
| C、15° | D、45° |
圆柱的侧面展开图是一个边长为6π和4π的矩形,则该圆柱的底面积是( )
| A、24π2 |
| B、36π2和16π2 |
| C、36π |
| D、9π和4π |
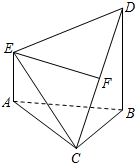 如图,在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,BD∥AE,BD=2AE.
如图,在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,BD∥AE,BD=2AE.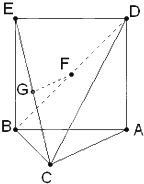 三角形ABC中,AC=BC=
三角形ABC中,AC=BC=