题目内容
 已知函数f(x)=
已知函数f(x)=
|
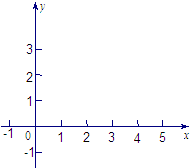
(1)在如图所示给定的直角坐标系内画出f(x)的图象;
(2)写出f(x)的单调递增区间;
(3)由图象指出当x取什么值时f(x)有最值.
考点:函数的最值及其几何意义,函数图象的作法,函数单调性的判断与证明
专题:函数的性质及应用
分析:本题考查的是分段函数问题.在解答时,对(1)应先根据自变量的范围不同根据相应的解析式画出不同段上的函数图象,进而问题即可获得解答;
对(2)充分利用第一问中函数的图象即可直观的看出函数的单调递增区间,注意多个单调区间之间用逗号隔开或用和连接,
(3)由图象可以直接观察得到.
对(2)充分利用第一问中函数的图象即可直观的看出函数的单调递增区间,注意多个单调区间之间用逗号隔开或用和连接,
(3)由图象可以直接观察得到.
解答:
解:(1)由题意可知:
当x∈[-1,2]时,f(x)=-x2+3,为二次函数的一部分;
当x∈(2,5]时,f(x)=x-3,为一次函数的一部分;
所以,函数f(x)的图象如图所示;
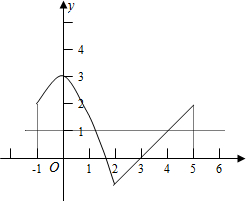
(2)由函数的图象可知:
函数f(x)的单调递增区间为:[-1,0]和[2,5].
(3)由图象可知,当x=1时有最大值3;当x=2时,f(x)min=-1.
当x∈[-1,2]时,f(x)=-x2+3,为二次函数的一部分;
当x∈(2,5]时,f(x)=x-3,为一次函数的一部分;
所以,函数f(x)的图象如图所示;

(2)由函数的图象可知:
函数f(x)的单调递增区间为:[-1,0]和[2,5].
(3)由图象可知,当x=1时有最大值3;当x=2时,f(x)min=-1.
点评:本题考查的是分段函数问题.在解答的过程当中充分体现了函数图象的画法、单调性的分析以及问题转化和画图读图的能力.值得同学们体会反思.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
圆心角为135°,面积为B的扇形围成一个圆锥,若圆锥的全面积为A,则A:B等于( )
| A、11:8 | B、3:8 |
| C、8:3 | D、13:8 |
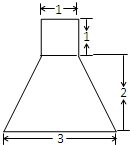
已知某空间几何体的正视图和侧视图相同,且如图所示,俯视图是两个同心圆,则它的表面积为( )

A、
| ||||
B、(12+4
| ||||
C、
| ||||
D、(13+4
|
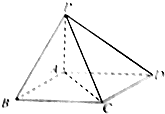 如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,且PA=AD=2,AB=1,AC=
如图所示,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,且PA=AD=2,AB=1,AC=