题目内容
已知关于x的方程cosx+sin2x+m-1=0（m∈R）恒有实数解，记m的所有可能取构成集合M，若λ为区间[-1，4]上的随机数，则λ∈M的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：根据方程cosx+sin2x+m-1=0（m∈R）恒有实数解，求出m的取值范围，根据几何概型的概率公式进行求解即可．
解答：
解：由cosx+sin2x+m-1=0得m=cosx2-cosx=（cosx-
）2-
，
∵-1≤cosx≤1，
∴-
≤m≤2，
即M=[-
，2]，
若λ为区间[-1，4]上的随机数，
则λ∈M的概率P=
=
，
故选：D
| 1 |
| 2 |
| 1 |
| 4 |
∵-1≤cosx≤1，
∴-
| 1 |
| 4 |
即M=[-
| 1 |
| 4 |
若λ为区间[-1，4]上的随机数，
则λ∈M的概率P=
2-(-
| ||
| 4-(-1) |
| 9 |
| 20 |
故选：D
点评：本题主要考查几何概型的概率公式的应用，根据条件求m的等价条件是解决本题的关键．
练习册系列答案
相关题目
已知函数f（x），g（x）均为[a，b]上的可导函数，在[a，b]上连续且f′（x）＜g′（x），则f（x）-g（x）的最大值为（ ）
| A、f（a）-g（a） |
| B、f（b）-g（b） |
| C、f（a）-g（b） |
| D、f（b）-g（a） |
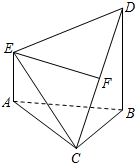如图，在四棱锥C-ABDE中，F为CD的中点，DB⊥平面ABC，BD∥AE，BD=2AE．