题目内容

设A（x1，y1）、B（x2，y2）、C（x3，y3）是抛物线x2=2py（p＞0﹚上的三点，F是其焦点，且x12、x22、x32成等差数列．求证：|AF|、|BF|、|CF|也成等差数列．
考点：抛物线的简单性质,直线与圆锥曲线的综合问题
专题：圆锥曲线的定义、性质与方程
分析：由x12，x22，x32成等差数列得到2x22=x12+x32，转化为点的纵坐标的关系后结合抛物线的定义转化为焦半径：|AF|、|BF|、|CF|的关系，即2|BF|=|AF|+|CF|．从而证明：|AF|、|BF|、|CF|也等差数列．
解答： 证明：∵x12，x22，x32成等差数列，
∴2x22=x12+x32，
即4py2=2py1+2py3，
∴2y2=y1+y3，则2(y2+
p
2
)=y1+
p
2
+y3+
p
2
，
由抛物线的定义知：|AF|=y1+
p
2
，|BF|=y2+
p
2
，|CF|=y3+
p
2
，
∴2|BF|=|AF|+|CF|．
即：|AF|、|BF|、|CF|成等差数列．
点评：本题是直线与圆锥曲线综合题，考查抛物线的定义及焦半径公式，体现了数学转化思想方法，是中档题．
练习册系列答案
相关题目
函数f（x）=
x(8-3x)
的最大值为
 
．
设f（x）可导，且y=f（e2x），则y′=（　　）
A、f′（e2x）
B、f′（e2x）e2x
C、2f′（e2x）
D、2f′（e2x）e2x
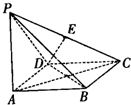设A是圆形纸片内不同于圆心的一个点，取圆周上一点B，折叠纸片使点B与A重合，得到一条折痕，当点B取遍圆周上所有点时，得到的所有折痕均与某条曲线相切，这条曲线是一个（　　）
A、圆B、椭圆C、双曲线D、抛物线
四棱锥P-ABCD的底面为棱形，且∠DAB=60°，PA⊥底面ABCD，AB=2a，PA=2
3
a，E为PC的中点．
（1）求直线DE与平面PAC所成角的大小；
（2）求二面角E-AD-C的余弦值．
已知椭圆的中心在原点，焦点在x轴上，长轴是短轴的2倍，且过点E（
8
5
，
3
5
），又知一圆的方程为（x-1）2+y2=9
（1）求椭圆的方程；
（2）证明存在不垂直于x轴的直线l与已知圆交于A、B两点，与椭圆交于C、D两点，且满足|
AC
|=|
BD
|，并求|
AB
|的范围．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点为F（1，0），短轴的一个端点B到F的距离等于焦距．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点F的直线l与椭圆C交于不同的两点M，N，是否存在直线l，使得△BFM与△BFN的面积比值为2？若存在，求出直线l的方程；若不存在，说明理由．
已知实数x，y满足y=
3-x2+2x
，求z=
y+3
x-1
的取值范围．
已知f（x）=
1
2x+
2
，求S=f（-10）+f（-9）+…+f（0）+…+f（10）+f（11）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网