Question

已知实数x，y满足y=

3-x2+2x

，求z=

y+3

x-1

的取值范围．

Answer 1

考点：直线与圆的位置关系

专题：直线与圆

分析：作出函数y的图象，利用z的几何意义，利用直线和圆的位置关系，结合数形结合即可得到结论．

解答： 解：由y=

3-x2+2x

得y²=3-x²+2x，
即（x-1）²+y²=4，（y≥0），则函数对应的曲线为圆心为（1，0），半径为2的上半圆，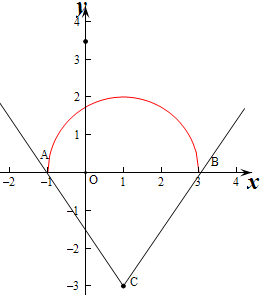
由z=

y+3

x-1

则z的几何意义，为圆上的点到定点C（1，-3）的斜率，
由图象可知A（-1，0），B（3，0），
则AC的斜率k=

3

-2

=-

3

2

，
BC的斜率k=

3

3-1

=

3

2

，
∴z满足z≥

3

2

或z≤-

3

2

..

点评：本题主要考查直线和圆的位置关系的应用以及直线斜率的计算，利用数形结合是解决本题的关键．